题目内容
【题目】已知f(x)是R上的奇函数，当x＞0时，解析式为f(x)＝
.
(1)求f(x)在R上的解析式；
(2)用定义证明f(x)在(0，＋∞)上为减函数．
【答案】(1) f(x)＝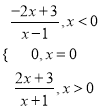
(2)见解析
【解析】试题分析：（1）分别求出当x＜0和x=0时的解析式，写成分段函数的形式；（2）设x1，x2∈(0，＋∞)，且x1＜x2，通过作差证明f(x1)＞f(x2)即可。
试题解析：(1)设x＜0，则－x＞0，
∴f(－x)＝
.
又∵f(x)是R上的奇函数，
∴f(－x)＝－f(x)＝，
∴f(x)＝
.
又∵奇函数在x=0时有意义，
∴f(0)＝0，
∴函数的解析式为f(x)＝
(2)证明：设x1，x2∈(0，＋∞)，且x1＜x2，
则f(x1)－f(x2)＝
－
＝
＝
.
∵x1，x2∈(0，＋∞)，x1＜x2，
∴x1＋1＞0，x2＋1＞0，x2－x1＞0，
∴f(x1)－f(x2)＞0，
∴f(x1)＞f(x2)，
∴函数f(x)在(0，＋∞)上为减函数．
练习册系列答案
阅读快车系列答案
相关题目
