题目内容

已知向量a=(1-tanx,1),b=(1+sin2x+cos2x,-3),记f(x)=a·b.

(1)求f(x)的定义域,值域及最小正周期；

(2)若f()-f(+)=,其中α∈(0,),求α.

解:(1)f(x)=(1-tanx)(1+sin2x+cos2x)-3=·(2cos2x+2sinxcosx)-3=2(cos2x-sin2x)-3=2cos2x-3.                                                                                               ?

∴定义域为{x|x≠kπ+,k∈Z}.                                                                         ?

值域为(-5,-1］.                                                                                                       ?

最小正周期T=π.                                                                                                     ?

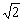(2)f()-f(+)=2cosα-2cos(α+)=2(cosα+sinα)=2Equation.3sin(α+)=.      ?

∴sin(α+)=.?

∵α∈(0,),∴α+∈(,).?

∴α+=或α+=.?

∴α=或α=.


练习册系列答案
相关题目
已知向量
a
=(1，t)，
b
=(-1，t)，若2
a
-
b
与
b
垂直，则|
a
|=
 
．
有下列命题：
①如果幂函数f （x）=（m2-3m+3）xm2-m-1的图象不过原点，则m=l或2；
②数列{an}为等比数列的充要条件为an=a1qn-1（q为常数）：
③已知向量
a
=（t，2），
b
=（-3，6），若向量
a
与
b
的夹角为锐角，则实数t的取值范围是t＜4； 
④函数f （x）=xsinx在（0，π）上有最大值，没有最小值．
其中正确命题的个数为（　　）
已知向量
a
=(1-t，2t-1，0)与
b
=(2，t，t)，则|
b
-
a
|的最小值是
2
2
．
已知向量
a
=(1-t，  2t-1，  0)，
b
=(2，  t，  t)，则|
a
-
b
|的最小值是（　　）
A、
2
B、
3
C、3
D、2
已知向量
a
=(1-t，2t-1，0)与
b
=(2，t，t)，则|
b
-
a
|的最小值是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网