题目内容
1.已知函数y=x+$\frac{a}{x}$有如下性质:如果a>0,那么该函数在(0,$\sqrt{a}$]上是减函数,在[$\sqrt{a}$,+∞)上是增函数.(1)若函数y=x+$\frac{{3}^{m}}{x}$(x>0)的值域是[6,+∞),求实数m的值;
(2)若把函数f(x)=x2+$\frac{a}{{x}^{2}}$(a>0)在[1,2]上的最小值记为g(a).
(ⅰ)求g(a)的表达式;
(ⅱ)若g(a)≥t2-mt-1对所有的a>0,m∈[-1,1]恒成立,求实数t的取值范围.
分析 (1)由给出的性质可得x=$\sqrt{{3}^{m}}$,取得最小值6,解方程可得m=2;
(2)(ⅰ)令x2=t,则$f(t)=t+\frac{a}{t}$.于是原题即求f(t)在[1,4]上的最小值.对a讨论,①当$\sqrt{a}>4$,②当$1≤\sqrt{a}≤4$,③当$\sqrt{a}<1$,运用单调性,可得最小值;
(ⅱ)由①得当a>0时,g(a)>1,要使g(a)≥t2-mt-1对所有的a>0,m∈[-1,1]恒成立,只要t2-mt-1≤1,由一次函数的单调性,可得不等式,即可解得t的范围.
解答 解:(1)由已知,函数$y=x+\frac{3^m}{x}({x>0})$在$({0,\sqrt{3^m}}]$上是减函数,
在$[{\sqrt{3^m},+∞})$上是增函数,
∴${y_{min}}=\sqrt{3^m}+\frac{3^m}{{\sqrt{3^m}}}=2\sqrt{3^m}$,
∴$2\sqrt{3^m}=6$,3m=9,∴m=2.
(2)(ⅰ)令x2=t,∵x∈[1,2],∴t∈[1,4].
则$f(t)=t+\frac{a}{t}$.
于是原题即求f(t)在[1,4]上的最小值.
①当$\sqrt{a}>4$,即a>16时,f(t)在[1,4]上是减函数,此时$g(a)=f(4)=4+\frac{a}{4}$;
②当$1≤\sqrt{a}≤4$,即1≤a≤16时,$g(a)=f({\sqrt{a}})=2\sqrt{a}$;
③当$\sqrt{a}<1$,即0<a<1时,f(t)在[1,4]上是增函数,此时g(a)=f(1)=1+a.
综上,$g(a)=\left\{\begin{array}{l}1+a,0<a<1\\ 2\sqrt{a},1≤a≤16\\ 4+\frac{a}{4},a>16.\end{array}\right.$;
(ⅱ)由①得当a>0时,g(a)>1,
∴要使g(a)≥t2-mt-1对所有的a>0,m∈[-1,1]恒成立,只要t2-mt-1≤1,
即t2-mt-2≤0对所有的m∈[-1,1]恒成立.
令h(m)=t2-mt-2,则$\left\{\begin{array}{l}h({-1})≤0\\ h(1)≤0\end{array}\right.$,即$\left\{\begin{array}{l}{t^2}+t-2≤0\\{t^2}-t-2≤0\end{array}\right.$,解得-1≤t≤1.
∴实数t的取值范围是[-1,1].
点评 本题考查函数的最值的求法,考查不等式恒成立问题的解法,考查分类讨论和运算求解能力,属于中档题.

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 |
| 平均气温x(°C) | 29 | 26 | 24 | 22 | 20 |
| 销量y(件) | 11 | 8 | 7 | 5 | 3 |
(1)求选取的2组数据恰好是相邻2天数据的概率;
(2)若选取的是10月1日至2日的两组数据,请根据10月3日至10月5日的数据,求出y关于x的线性回归方程$\hat y=bx+a$;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2件,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 命题“存在x∈R,x2-x>0”的否定是:“任意x∈R,x2-x≤0” | |
| C. | 命题“p或q”为真命题,则命题“p”和命题“q”均为真命题 | |
| D. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 |
| A. | (2,0) | B. | (0,2) | C. | 2 | D. | 0 |
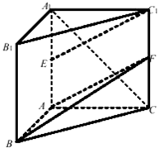 如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.
如图,在直三棱柱ABC-A1B1C1中,AB⊥AC,AB=AC=$\frac{\sqrt{2}}{2}A{A}_{1}$,E是棱A1A的中点,F为棱CC1上的一动点.