题目内容
若△ABC顶点B，C的坐标分别为（-4，0），（4，0），AC，AB边上的中线长之和为30，则△ABC的重心G的轨迹方程为（ ）
分析：根据三角形重心的性质可得G到B、C两点的距离之和等于20，因此G的轨迹为以B、C为焦点的椭圆．利用题中数据加以计算可得相应的椭圆方程，注意到点G不能落在x轴上得到答案．
解答：解：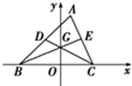
设AC、AB边上的中线分别为CD、BE
∵BG=
BE，CG=
CD
∴BG+CG=
（BE+CD）=20（定值）
因此，G的轨迹为以B、C为焦点的椭圆，2a=20，c=4
∴a=10，b=
=
，可得椭圆的方程为
+
=1
∵当G点在x轴上时，A、B、C三点共线，不能构成△ABC
∴G的纵坐标不能是0，可得△ABC的重心G的轨迹方程为
+
=1（y≠0）
故选：D
设AC、AB边上的中线分别为CD、BE∵BG=
| 2 |
| 3 |
| 2 |
| 3 |
∴BG+CG=
| 2 |
| 3 |
因此，G的轨迹为以B、C为焦点的椭圆，2a=20，c=4
∴a=10，b=
| a2-c2 |
| 84 |
| x2 |
| 100 |
| y2 |
| 84 |
∵当G点在x轴上时，A、B、C三点共线，不能构成△ABC
∴G的纵坐标不能是0，可得△ABC的重心G的轨迹方程为
| x2 |
| 100 |
| y2 |
| 84 |
故选：D
点评：本题给出三角形两条中线长度之和等于定值，求重心G的轨迹方程．着重考查了三角形重心的性质、椭圆的定义与标准方程和轨迹方程的求法等知识，属于中档题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
+
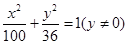=1(y≠0) B.
+
=1(y≠0)
+
=1(x≠0) D.
+
=1(x≠0)
+
=1(y≠0) B.
=1(y≠0)
B．
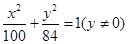
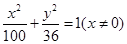D．