Question

双曲线

x2

a2

-

y2

b2

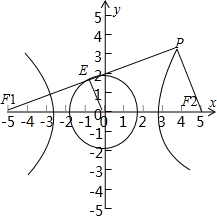
=1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，过左焦点F₁作圆x²+y²=

1

4

a²的切线，切点为E，直线EF₁交双曲线右支于点P．若

OE

=

1

2

（

OF1

+

OP

），则双曲线的离心率是（　　）

• A、

  10

• B、2

  2

• C、

  10

  2

• D、

  2

Answer 1

考点：双曲线的简单性质

专题：综合题,圆锥曲线的定义、性质与方程

分析：先确定E为F₁P的中点，所以OE为△PF₁F₂的中位线，进而得到|PF₂|=a，|F₁F₂|=2c，|PF₁|=2a+a=3a，PF₁切圆O于E，可得PF₂⊥PF₁，由勾股定理得出关于a，c的关系式，最后即可求得离心率．

解答： 解：∵

OE

=

1

2

（

OF1

+

OP

），
∴E为F₁P的中点，
∵O为F₁F₂的中点，
∴OE为△PF₁F₂的中位线，
∴OE∥PF₂，|OE|=

1

2

|PF₂|，
∵|OE|=

1

2

a
∴|PF₂|=a
∵PF₁切圆O于E
∴OE⊥PF₁
∴PF₂⊥PF₁，
∵|F₁F₂|=2c，|PF₁|-|PF₂|=2a⇒|PF₁|=2a+a=3a，
∴由勾股定理a²+9a²=4c²
∴10a²=4c²，
∴e=

c

a

=

10

2

．
故选：C．

点评：本题主要考查双曲线的标准方程，以及双曲线的简单性质的应用等基础知识，考查运算求解能力，考查化归与转化思想．属于中档题．