题目内容
讨论函数f(x)＝(
)
的单调性，并求其值域．
答案：
解析：
解析：
解：
函数的定义域为(－∞，＋∞)，设x1、x2∈(－∞，＋∞)，且x1＜x2． 则f(x1)＝(
)
＞0，f(x2)＝()
＞0，
．
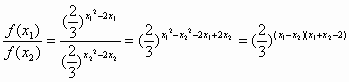当x1＜x2≤1时，x1＋x2＜2，即有x1＋x2－2＜0．
又因为x1－x2＜0，
所以(x1－x2)(x1＋x2－2)＞0，则0＜()
＜1，
又对于任意的实数x，f(x)＞0，
所以f(x1)＜f(x2)．
所以函数f(x)＝()
在(－∞，1]上是增函数．
当1≤x1＜x2时，x1＋x2＞2，即有x1＋x2－2＞0，
又因为x1－x2＜0，
所以(x1－x2)(x1＋x2－2)＜0，则()＞1．
又对于任意的实数x，f(x)＞0，
所以f(x1)＞f(x2)．
所以函数f(x)＝()
在[1，＋∞)上是减函数．
综上，可知函数f(x)＝()在(－∞，1]上是增函数，在[1，＋∞)上是减函数．
因为x2－2x＝(x－1)2－1≥－1，0＜＜1，
所以0＜()≤()－1＝
，即函数的值域为(0，]．
思路分析：对于任意的实数x，()
＞0恒成立，则在讨论函数的单调性时，可用作商法比较大小．求函数的值域可利用指数函数的单调性．
练习册系列答案
相关题目
的单调性，并求其值域．
与x＝－1是f(x)的极值点．
)x2＋2x的单调性，并求其值域．