题目内容
设sin(![]() -x)=
-x)=![]() ,0<x<
,0<x<![]() ,求
,求 的值.
的值.
答案:
解析:
提示:
解析:
|
解法1:∵0<x< ∴cos( = 又cos( ∴原式= = =2cos( 解法2:cos2x=cos2x-sin2x=(cosx+sinx)·(cosx-sinx) = =2sin(x+ ∴原式= =2sin(x+ 后面同解法一. 思路分析:注意到角之间的关系,2x是x的二倍角, |
提示:
|
仔细分析角与角的关系,如 |

练习册系列答案
相关题目



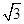 cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为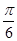 .
.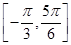 上的最小值为
上的最小值为 .
. ,x∈R,则f(x)是( )
,x∈R,则f(x)是( ) 的奇函数
的奇函数