题目内容
（本题满分12分）
已知函数f(x)=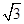
cos2x+sinxcosx
.
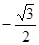（1）求函数f（x）的单调递增区间；
(2)若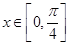
，求函数f（x）的取值范围；
已知函数f(x)=
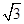cos2x+sinxcosx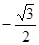.（1）求函数f（x）的单调递增区间；
(2)若
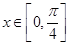，求函数f（x）的取值范围；（1）
（2）
（2）试题分析：解：(1)
所以
的单调递增区间为
点评：解决的关键是能利用三角恒等变换，以及函数的性质准确的求解，属于基础题。
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
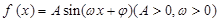的图象如图所示，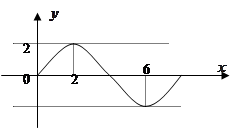
．
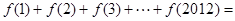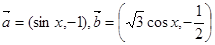，函数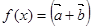
·
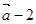
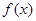的最小正周期T及单调减区间
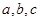分别是△ABC内角A，B，C的对边，其中A为锐角，
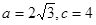且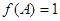
，求A，b和△ABC的面积S
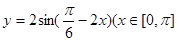)为增函数的区间是（ ）
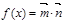其中
，
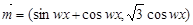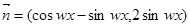
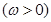，若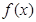
图象中相邻的两条对称轴间的距离不小于
。
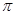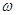的取值范围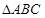
中，a,b,c分别为角A，B，C的对边，
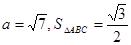。当
的图象，只要将函数
的图象( ) 
单位
单位
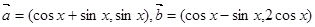,设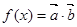
.
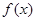的最小正周期，并写出
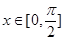时,求函数
最小正周期为
的单调递增区间及对称中心坐标
上的取值范围。