题目内容

(Ⅰ) 解析:设点![]() 的坐标为
的坐标为![]()
![]() ,
,
由于抛物线![]() 和圆
和圆![]() 关于
关于![]() 轴对称,故点
轴对称,故点![]() 的坐标为
的坐标为![]() .
.
![]()
![]()
,![]() , 即
, 即![]() .
.
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,![]()
![]() .
.
![]() , 即
, 即![]() .
.
![]() .
.![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 在圆
在圆![]() 上,
上,![]() ,又
,又![]() ,解得
,解得![]() .
.
(Ⅱ) 解法1:设直线![]() 的方程为:
的方程为:![]() ,因为
,因为![]() 是圆O的切线,则有
是圆O的切线,则有![]() ,
,
又![]() ,则
,则![]() .
.
即![]() 的方程为:
的方程为:![]() .
.
联立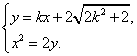
即![]() .
.
设![]() ,则
,则![]() .
.
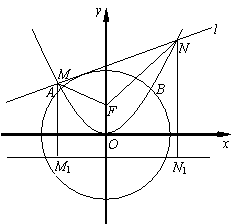
如图,设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,作
,作![]() ,垂足分别为
,垂足分别为![]() .
.
由抛物线的定义有:
![]()
![]()
![]() .
.
令![]() ,则
,则![]() .∴
.∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴当![]() 时,
时,![]() 有最大值11.
有最大值11.
当![]() 时,
时,![]() ,故直线
,故直线![]() 的方程为
的方程为![]() .
.
解法2:设直线![]() 与圆
与圆![]() 相切的切点坐标为
相切的切点坐标为![]() ,则切线
,则切线![]() 的方程为
的方程为![]() .
.
由![]() 消去
消去![]() ,得
,得![]() .
.
设![]() ,则
,则![]() .
.
如图,设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,作
,作![]() ,垂足分别为
,垂足分别为![]() .
.
由抛物线的定义有:
![]()
![]()
![]() .
.
![]() ,
,
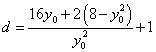
![]()
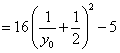 .
.
![]() ,
,![]() 当
当![]() 时,
时,![]() 有最大值11.
有最大值11.
当![]() 时,
时,![]() ,故直线
,故直线![]() 的方程为
的方程为![]() .
.

练习册系列答案
相关题目
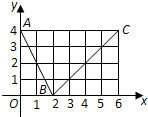 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(f(0))=