题目内容
设e1,e2是两个互相垂直的单位向量,且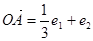 ,
,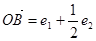 则
则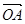 在
在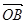 上的投影为( )
上的投影为( )
A.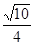 | B.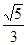 | C.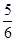 | D.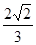 |
B
解析试题分析:因为e1,e2是两个互相垂直的单位向量,所以 ,
, 。
。
由于
 ,
, ,
, ,设向量
,设向量 的夹角为
的夹角为 ,则由
,则由 得:
得: =
= 。故选B。
。故选B。
考点:向量的投影
点评:本题需要理解数量积的几何意义:向量 与
与 的数量积等于向量
的数量积等于向量 (
( )的模乘以向量
)的模乘以向量 (
( )在向量
)在向量 (
( )方向上的投影
)方向上的投影 (
( )。
)。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知向量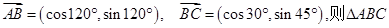 的形状为( )
的形状为( )
| A.直角三角形 | B.等腰三角形 | C.锐角三角形 | D.钝角三角形 |
已知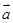 、
、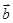 是平面向量,若
是平面向量,若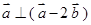 ,
,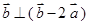 ,则
,则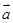 与
与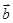 的夹角是( )
的夹角是( )
A.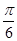 | B.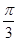 | C.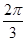 | D.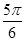 |
若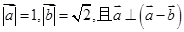 ,则向量
,则向量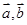 的夹角为
的夹角为
| A.45° | B.60° | C.120° | D.135° |
已知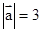 ,
,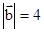 ,且(
,且(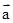 +k
+k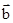 )⊥(
)⊥(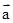
 k
k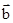 ),则k等于 ( )
),则k等于 ( )
A.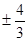 | B.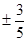 | C.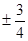 | D.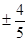 |
已知向量 ,
, 满足|
满足| |="2," |
|="2," |  |=l,且(
|=l,且( +
+ )⊥(
)⊥(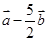 ),则
),则 与
与 的夹角为
的夹角为
A.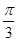 | B.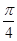 | C.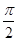 | D.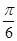 |
平面向量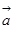 与
与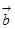 的夹角为
的夹角为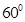 ,
,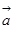 =(2,0),
=(2,0),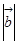 ="1" 则
="1" 则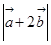 =( )
=( )
A. | B.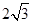 | C.4 | D.12 |
 的边长为
的边长为 ,
,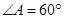 ,
, 为
为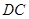 的中点,则
的中点,则 的值为 .
的值为 .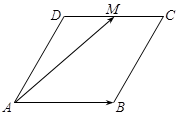
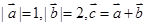 ,且
,且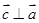 ,则向量
,则向量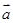 与
与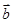 的夹角为( )
的夹角为( )