题目内容
如图,菱形 的边长为
的边长为 ,
,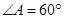 ,
, 为
为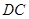 的中点,则
的中点,则 的值为 .
的值为 .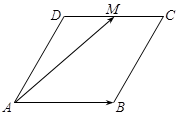
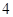
解析试题分析:根据题意,由于菱形 的边长为
的边长为 ,
,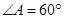 ,
, 为
为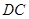 的中点,先以点A位坐标原点建立的直角坐标系,求出其它各点的坐标,然后利用点的坐标表示出
的中点,先以点A位坐标原点建立的直角坐标系,求出其它各点的坐标,然后利用点的坐标表示出
,把所求问题转化为在平面区域内求线性目标函数的最值问题求解即可。解::以点A位坐标原点建立如图所示的直角坐标系,由于菱形ABCD的边长为2,∠A=60°,M为DC的中点,故点A(0,0),则B(2,0),C(3, ),D(1,
),D(1, ),M(2,
),M(2, )
)
设N(x,y),N为平行四边形内(包括边界)一动点,对应的平面区域即为平行四边形ABCD及其内部区域. =4,故可知答案为4.
=4,故可知答案为4.
考点:向量在几何中的应用
点评:本题主要考查向量在几何中的应用以及数形结合思想的应用和转化思想的应用,是对基础知识和基本思想的考查,属于中档

练习册系列答案
相关题目
平面向量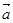 与
与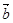 的夹角为60°,
的夹角为60°,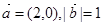 ,则
,则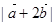 等于 ( )
等于 ( )
A.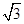 | B.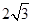 | C.4 | D.12 |
平面四边形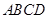 中
中 ,
, ,则四边形
,则四边形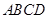 是 ( )
是 ( )
| A.矩形 | B.梯形 | C.正方形 | D.菱形 |
已知A=(1,-2),若向量 与a=(2,-3)反向,|
与a=(2,-3)反向,| |=4
|=4 ,则点B的坐标为( )
,则点B的坐标为( )
| A.(10,7) | B.(-10,7) | C.(7,-10) | D.(-7,10) |
已知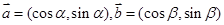 则 ( )
则 ( )
A.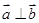 | B.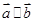 |
C.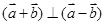 | D.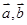 的夹角为 的夹角为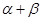 |
在△ABC中,∠C=90°, 则k的值是( )
则k的值是( )
| A.5 | B.-5 | C. | D. |
设e1,e2是两个互相垂直的单位向量,且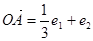 ,
,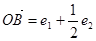 则
则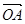 在
在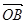 上的投影为( )
上的投影为( )
A.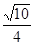 | B.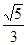 | C.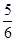 | D.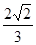 |
若向量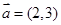 ,
,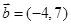 ,则
,则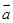 在
在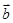 方向上的投影为( )
方向上的投影为( )
A.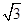 | B.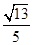 | C.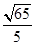 | D.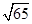 |
若向量 和向量
和向量 平行,则
平行,则  ( )
( )
A. | B. | C. | D. |