题目内容
)如图所示,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯

形,∠BAD=∠FAB=90°,BC![]()
![]() AD,BE
AD,BE![]()
![]() FA,G、H分别为FA、FD的中点.
FA,G、H分别为FA、FD的中点.
(1)证明:四边形BCHG是平行四边形;
(2)C、D、F、E四点是否共面?为什么?
(3)设AB=BE,证明:平面ADE⊥平面CDE.
证明略
解析:
方法一 (1) 由题设知,FG=GA,
FH=HD,所以GH![]()
![]() AD.
AD.
又BC![]()
![]() AD,故GH
AD,故GH![]() BC.
BC.
所以四边形BCHG是平行四边形.
(2) C、D、F、E四点共面.
理由如下:
由BE![]() AF,G是FA的中点知,
AF,G是FA的中点知,
BE ![]() GF,所以EF∥BG.
GF,所以EF∥BG.
由(1)知BG∥CH,所以EF∥CH,故EC、FH共面.
又点D在直线FH上,所以C、D、F、E四点共面.
(3)如图,连接EG,由AB=BE,BE![]() AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.
AG及∠BAG=90°知ABEG是正方形,故BG⊥EA.
由题设知,FA、AD、AB两两垂直,故AD⊥平面FABE,
 因此EA是ED在平面FABE内的射影,根据三垂线定理,BG⊥ED.
因此EA是ED在平面FABE内的射影,根据三垂线定理,BG⊥ED.
又ED∩EA=E,所以BG⊥平面ADE.
由(1)知,CH∥BG,所以CH⊥平面ADE.
由(2)知CH![]() 平面CDE,得平面ADE⊥平面CDE.
平面CDE,得平面ADE⊥平面CDE.
方法二 由题设知,FA、AB、AD两两互相垂直.
如图,以A为坐标原点,射线AB为x轴正方向,以射线AD为y轴正方向,
以射线AF为z轴正方向,建立直角坐标系A—xyz.
(1) 设AB=a,BC=b,BE=c,则由题设得
 A(0,0,0),B(a,0,0),C(a,b,0),D(0,2b,0),E(a,0,c),
A(0,0,0),B(a,0,0),C(a,b,0),D(0,2b,0),E(a,0,c),
G(0,0,c),H(0,b,c).
所以,![]() =(0,b,0),
=(0,b,0),![]() =(0,b,0),于是
=(0,b,0),于是![]() =
=![]() .
.
又点G不在直线BC上,
所以四边形BCHG是平行四边形.
(2) C、D、F、E四点共面.
理由如下:由题设知F(0,0,2c),
所以![]() =(-a,0,c),
=(-a,0,c),![]() =(-a,0,c),
=(-a,0,c),![]() =
=![]() .
.
又C![]() EF,H∈FD,故C、D、F、E四点共面.
EF,H∈FD,故C、D、F、E四点共面.
(3) 由AB=BE,得c=a,
所以![]() =(-a,0,a),
=(-a,0,a),![]() =(a,0,a).
=(a,0,a).
又![]() =(0,2b,0),因此
=(0,2b,0),因此![]() ·
·![]() =0,
=0,![]() ·
·![]() =0.
=0.
即CH⊥AE,CH⊥AD.
又AD∩AE=A,所以CH⊥平面ADE.
故由CH![]() 平面CDFE,得平面ADE⊥平面CDE.
平面CDFE,得平面ADE⊥平面CDE.

 6、如图所示,平面α∩平面β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是( )
6、如图所示,平面α∩平面β=l,A∈α,B∈α,AB∩l=D,C∈β,C∉l,则平面ABC与平面β的交线是( ) 11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD=
11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD=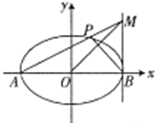 如图所示,平面直角坐标系中,已知椭圆
如图所示,平面直角坐标系中,已知椭圆 如图所示,平面α∩平面β=l,点A、B∈α,点C∈β,AB∩l=R,设过A、B、C三点的平面为γ,则β∩γ是( )
如图所示,平面α∩平面β=l,点A、B∈α,点C∈β,AB∩l=R,设过A、B、C三点的平面为γ,则β∩γ是( ) 如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,BD⊥l,AB=3cm,AC=5cm,BD=4cm,则CD与平面N所成角的大小为
如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,BD⊥l,AB=3cm,AC=5cm,BD=4cm,则CD与平面N所成角的大小为