题目内容
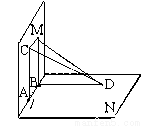
 如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,BD⊥l,AB=3cm,AC=5cm,BD=4cm,则CD与平面N所成角的大小为
如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,BD⊥l,AB=3cm,AC=5cm,BD=4cm,则CD与平面N所成角的大小为45°
45°
.分析:先根据平面M、N互相垂直且AC⊥l;得到AC⊥平面N,∠CAD即为所求;然后再通过求AD得到RT△CAD为等腰直角三角形,即可 得到结论.
解答:解:连接AD.
∵平面M、N互相垂直且AC⊥l;
∴AC⊥平面N,
∴∠CAD即为所求.
因为:BD⊥l,AB=3cm,AC=5cm,BD=4cm
∴AD=
=5.
∴RT△CAD,AC=AD=5为等腰直角三角形,
∴∠CAD=45°.
故答案为:45°
∵平面M、N互相垂直且AC⊥l;
∴AC⊥平面N,
∴∠CAD即为所求.
因为:BD⊥l,AB=3cm,AC=5cm,BD=4cm
∴AD=
| AB2+BD2 |
∴RT△CAD,AC=AD=5为等腰直角三角形,
∴∠CAD=45°.
故答案为:45°
点评:本题主要考查直线和平面所成的角.解决本题的关键在于根据平面M、N互相垂直且AC⊥l;得到AC⊥平面N,∠CAD即为所求.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD=
11、如图所示,平面M、N互相垂直,棱l上有两点A、B,AC?M,BD?N,且AC⊥l,AB=8cm,AC=6cm,BD=24cm,则CD=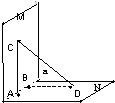 如图所示,平面M、N互相垂直,棱a上有两点A、B,AC?M,BD?N,且AC⊥a,BD⊥a,AB=12cm,AC=3cm,BD=4cm,则CD=
如图所示,平面M、N互相垂直,棱a上有两点A、B,AC?M,BD?N,且AC⊥a,BD⊥a,AB=12cm,AC=3cm,BD=4cm,则CD= M,BD
M,BD
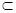 M,BD
M,BD