题目内容
 点D,E,F分别是△ABC三边AB,BC,CA的中点,
点D,E,F分别是△ABC三边AB,BC,CA的中点,
求证:(1) +
+ =
= +
+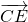 .
.
(2)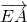 +
+ +
+ =
= .
.
证明:(1)由向量加法的三角形法则得, +
+ =
= ,
,
同理可得, +
+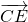 =
= ,
,
∴ +
+ =
= +
+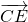 ,
,
(2)由向量加法的三角形法则得,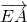 =
= ,
,
同理可得, =
= ,
, =
= ,
,
∴左边=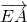 +
+ +
+ =
= +
+ +
+ =
= +
+ ①,
①,
∵点D,E,F分别是△ABC三边AB,BC,CA的中点,
∴ ,代入①得,左边=
,代入①得,左边= +
+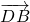 =
= ,
,
又∵ ,∴左边=
,∴左边= =右边,
=右边,
故等式成立.
分析:(1)利用图形和向量加法的三角形法则,证明左边等于右边;
(2)利用图形和向量加法的三角形法则,分别求出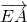 、
、 和
和 ,再把它们加在一起,由中点和向量相等证明出左边等于
,再把它们加在一起,由中点和向量相等证明出左边等于 .
.
点评:本题的考点是向量加法以及几何意义,主要考查了三角形法则以及向量相等的应用,注意利用图形进行化简和证明.
 +
+ =
= ,
,同理可得,
 +
+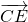 =
= ,
,∴
 +
+ =
= +
+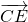 ,
,(2)由向量加法的三角形法则得,
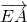 =
= ,
,同理可得,
 =
= ,
, =
= ,
,∴左边=
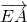 +
+ +
+ =
= +
+ +
+ =
= +
+ ①,
①,∵点D,E,F分别是△ABC三边AB,BC,CA的中点,
∴
 ,代入①得,左边=
,代入①得,左边= +
+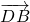 =
= ,
,又∵
 ,∴左边=
,∴左边= =右边,
=右边,故等式成立.
分析:(1)利用图形和向量加法的三角形法则,证明左边等于右边;
(2)利用图形和向量加法的三角形法则,分别求出
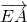 、
、 和
和 ,再把它们加在一起,由中点和向量相等证明出左边等于
,再把它们加在一起,由中点和向量相等证明出左边等于 .
.点评:本题的考点是向量加法以及几何意义,主要考查了三角形法则以及向量相等的应用,注意利用图形进行化简和证明.

练习册系列答案
相关题目
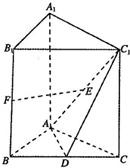 19、如图,在正三棱柱ABC-A1B1C1中,点D、E、F分别是BC、AC1、BB1的中点.
19、如图,在正三棱柱ABC-A1B1C1中,点D、E、F分别是BC、AC1、BB1的中点.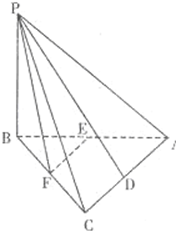 (2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.
(2012•广安二模)如图,在三棱锥P-ABC中,PB⊥面ABC,∠ABC=90°,AB=BC=2,∠PAB=45°,点D,E,F分别是AC,AB,BC的中点.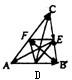 点D,E,F分别是△ABC三边AB,BC,CA的中点,求证:
点D,E,F分别是△ABC三边AB,BC,CA的中点,求证: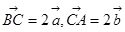 ,给出下列四个等式:①
,给出下列四个等式:①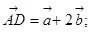 ②
②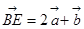 ;
;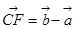 ;④
;④ .
.