题目内容
如右图，已知点D、E、F分别是△ABC三边AB、BC、CA的中点，求证：| EA |
| FB |
| DC |
| 0 |
分析：由题意先证明ADEF为平行四边形，再由向量加法的平行四边形法则得
+
=
，同理求出
，
再把三个式子加起来，重新组合利用向量加法的首尾相连法则求解．
| ED |
| EF |
| EA |
| FB |
| DC |
解答：
证明：连接DE、EF、FD，如图，
∵D、E、F分别是△ABC三边的中点，
∴EF∥AD，DE∥AF，
∴四边形ADEF为平行四边形，
由向量加法的平行四边形法则，得
+
=
①，
同理在平行四边形BEFD中，
+
=
②，
在平行四边形CFDE在中，
+
=
③，将①②③相加，得
(
+
+
=
+
+
+
+
+
=(
+
)+(
+
)+(
+
)
=
证明：连接DE、EF、FD，如图，∵D、E、F分别是△ABC三边的中点，
∴EF∥AD，DE∥AF，
∴四边形ADEF为平行四边形，
由向量加法的平行四边形法则，得
| ED |
| EF |
| EA |
同理在平行四边形BEFD中，
| FD |
| FE |
| FB |
在平行四边形CFDE在中，
| DF |
| DE |
| DC |
(
| EA |
| FB |
| DC |
| ED |
| EF |
| FD |
| FE |
| DE |
| DF |
=(
| EF |
| FE |
| ED |
| DE |
| FD |
| DF |
=
| 0 |
点评：本题的考点是向量的加法及其几何意义，根据图中的中点构成的中位线证明四边形是平行四边形，利用四边形法则，把所要证明的向量和转化为其他向量的和，由加法的首尾相连法则证出．
练习册系列答案
相关题目
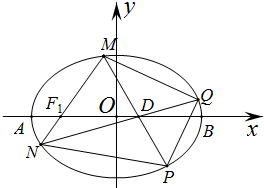如图，在平面直角坐标系xoy中，已知F1，F2分别是椭圆E：
如图，已知点P为椭圆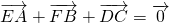
．
．