题目内容
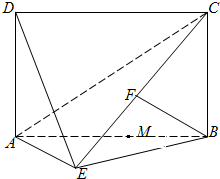
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=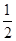 ,AD=1.
,AD=1.
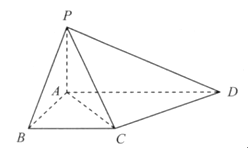
(I)求证:CD⊥平面PAC;
(II)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置,并证明,若不存在,请说明理由.
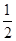 ,AD=1.
,AD=1.
(I)求证:CD⊥平面PAC;
(II)侧棱PA上是否存在点E,使得BE∥平面PCD?若存在,指出点E的位置,并证明,若不存在,请说明理由.
(I)见解析;(II)存在,证明见解析.
试题分析:(I)先根据已知条件证明
 ,那么就有
,那么就有 ,在根据题中已知边的长度,由勾股定理证明
,在根据题中已知边的长度,由勾股定理证明 ,根据直线与平面垂直的判定定理即可证明
,根据直线与平面垂直的判定定理即可证明 ;(II)设
;(II)设 的中点为
的中点为 , 连结
, 连结 ,
, ,
, ,证明四边形
,证明四边形 为平行四边形,由直线与平面平行的判定定理可知,
为平行四边形,由直线与平面平行的判定定理可知, 平面
平面 .
.试题解析:(I)∵
 ,∴
,∴ .
.又∵
 ,
, ,且
,且 ,
,∴
 .
. 又
 ,∴
,∴ . 3分
. 3分在底面
 中,∵
中,∵ ,
, ,
,∴
 ,有
,有 ,∴
,∴ .
.又∵
 , ∴
, ∴ . 6分
. 6分(II)在
 上存在中点
上存在中点 ,使得
,使得 平面
平面 , 8分
, 8分证明如下:设
 的中点为
的中点为 , 连结
, 连结 ,
, ,
, ,如图所示:
,如图所示:
则
 ,且
,且 .
. 由已知
 ,
, ,
,∴
 ,且
,且 , 10分
, 10分∴四边形
 为平行四边形,∴
为平行四边形,∴ .
.∵
 平面
平面 ,
, 平面
平面 ,
,∴
 平面
平面 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为矩形,
为矩形, 平面
平面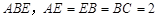 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
. 
 的体积;
的体积; 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 ,使得
,使得 平面
平面 .
. 中,
中, ,点
,点 在边
在边 上,点
上,点 在边
在边 上,且
上,且 ,垂足为
,垂足为 ,若将
,若将 沿
沿 折起,使点
折起,使点 位于
位于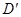 位置,连接
位置,连接 ,
, 得四棱锥
得四棱锥 .
.
 ;
; ,直线
,直线 与平面
与平面 所成角的大小为
所成角的大小为 ,求直线
,求直线 与平面
与平面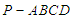 中,底面
中,底面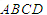 为菱形,
为菱形,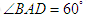 ,
,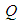 为
为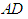 的中点。
的中点。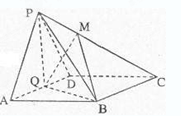
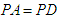 ,求证:平面
,求证:平面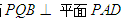 ;
;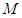 在线段
在线段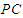 上,
上,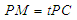 ,试确定
,试确定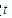 的值,使
的值,使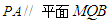 ;
;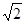 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,半径为1的鸡蛋(视为球体)放入其中,则鸡蛋中心(球心)与蛋巢底面的距离为 .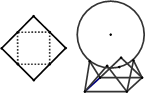
 为异面直线,
为异面直线, ,
,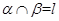 ,则直线
,则直线 ( )
( ) 是边长为
是边长为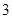 的
的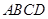 为正方形的对角线,将
为正方形的对角线,将 绕直线
绕直线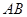 旋转一周后形成的几何体的体积等于 .
旋转一周后形成的几何体的体积等于 .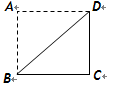
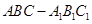 中,
中, 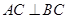 ,
, ,
,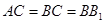 ,点
,点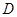 是
是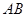 的中点,
的中点,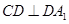 .
.
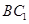 ∥平面
∥平面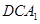 ;
;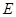 在线段
在线段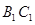 上,
上, ,且使直线
,且使直线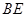 和平面
和平面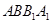 所成的角的正弦值为
所成的角的正弦值为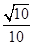 ,求
,求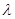 的值.
的值.  ,则正四棱锥的外接球的表面积为( )
,则正四棱锥的外接球的表面积为( )


