题目内容
如图,在四棱锥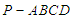 中,底面
中,底面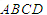 为菱形,
为菱形,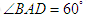 ,
,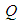 为
为 的中点。
的中点。
(1)若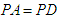 ,求证:平面
,求证:平面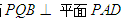 ;
;
(2)点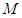 在线段
在线段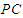 上,
上,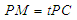 ,试确定
,试确定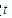 的值,使
的值,使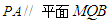 ;
;
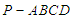 中,底面
中,底面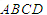 为菱形,
为菱形,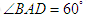 ,
,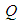 为
为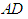 的中点。
的中点。
(1)若
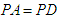 ,求证:平面
,求证:平面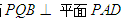 ;
;(2)点
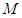 在线段
在线段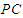 上,
上,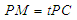 ,试确定
,试确定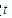 的值,使
的值,使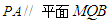 ;
;(1)证明详见解析;(2)

试题分析:(1)由已知条件可证AD⊥BQ,AD⊥PQ,根据平面与平面垂直的判定定理即可求证平面PQB⊥平面PAD.
(2)连结AC交BQ于N,由AQ∥BC,可证△ANQ∽△BNC,即得
 ,由直线与平面平行的性质,可证PA∥MN,即得
,由直线与平面平行的性质,可证PA∥MN,即得 ,所以PM=
,所以PM= PC,即t=
PC,即t= .
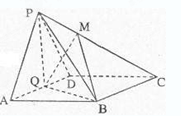
.试题解析:(1)连BD,四边形ABCD菱形, ∵AD⊥AB, ∠BAD="60°"
△ABD为正三角形, Q为AD中点, ∴AD⊥BQ
∵PA=PD,Q为AD的中点,AD⊥PQ
又BQ∩PQ=Q ∴AD⊥平面PQB, AD
 平面PAD
平面PAD ∴平面PQB⊥平面PAD;
(2)当
 时,
时, 平面
平面
下面证明,若
 平面
平面 ,连
,连 交
交 于
于
由
 可得,
可得, ,
,
 平面
平面 ,
, 平面
平面 ,平面
,平面 平面
平面 ,
,
 即:
即:
 ;
; 
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
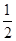 ,AD=1.
,AD=1.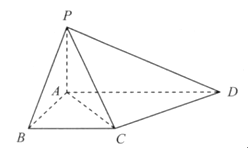
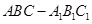 中,
中,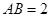 ,
,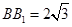 ,
,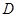 为
为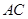 上的动点.
上的动点.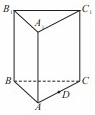
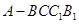 的体积;
的体积;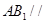 平面
平面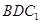 ,请说明理由;
,请说明理由;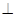 平面
平面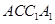 .
. 的底面
的底面 是正方形,棱
是正方形,棱 底面
底面 =1,
=1,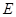 是
是 的中点.
的中点.
 平面
平面 ;
;  的余弦值.
的余弦值.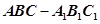 中,AB=BC,
中,AB=BC,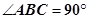 ,Q是AC上的点,AB1//平面BC1Q.
,Q是AC上的点,AB1//平面BC1Q.
 ,求二面角Q-BC1—C的余弦值.
,求二面角Q-BC1—C的余弦值. 的底面是边长为1的正六边形,
的底面是边长为1的正六边形, 底面
底面 。
。 平面
平面 ;
;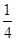 ,求六棱锥
,求六棱锥
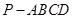 中,
中, 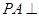 平面
平面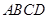 ,
,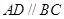 ,
,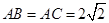 ,
,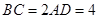 .
. 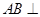 平面
平面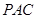 ;
;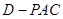 的高.
的高. 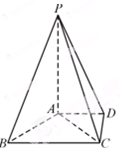
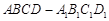 中,
中,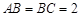 ,过
,过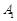 、
、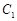 、
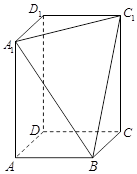
、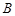 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体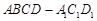 ,且这个几何体的体积为
,且这个几何体的体积为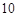 .
.
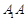 的长;
的长;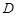 到平面
到平面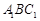 的距离.
的距离.