题目内容
D
(Ⅰ)解:由题意,可知椭圆的方程为![]() .
.
由已知得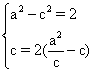
解得![]() ,c=2,
,c=2,
所以椭圆的方程为![]() ,离心率
,离心率![]() .
.
(Ⅱ)解:由(1)可得A(3,0).设直线PQ的方程为y=k(x-3).
联立方程组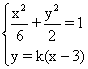 ,得(3k2+1)x2-18k2x+27k2-6=0,
,得(3k2+1)x2-18k2x+27k2-6=0,
依题意△=12(2-3k2)>0,得![]() .
.
设P(x1,y1),Q(x2,y2),则
![]() , ①
, ① ![]() . ②
. ②
由直线PQ的方程得为y1=k(x1-3),y2=k(x2-3),于是,
y1y2=k2(x1-3) (x2-3)= k2[x1x2-3(x1+ x2)+9]. ③
∵![]() ,∴x1x2+y1y2=0. ④
,∴x1x2+y1y2=0. ④
由①②③④得5k2=1,从而![]() .
.
所以直线PQ的方程为![]() 或
或![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
点P从(1,0)点出发,沿单位圆x2+y2=1按逆时针方向转动
弧长到达Q点,则Q的坐标为( )
| 2π |
| 3 |
A、(-
| ||||||
B、(-
| ||||||
C、(-
| ||||||
D、(-
|
y=2cosx的图象经过怎样的变换能变成函数y=2cos(2x+
)的图象( )
| π |
| 3 |
A、向左平移
| ||||
B、向左平移
| ||||
C、将图象上各点的横坐标缩短到原来的
| ||||
D、将图象上各点的横坐标伸长到原来的2倍,纵坐标不变,再向左平移
|
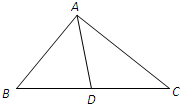 在△ABC中,AB=2,AC=3,D是边BC的中点,则
在△ABC中,AB=2,AC=3,D是边BC的中点,则