Question

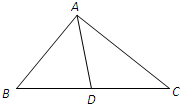在△ABC中，AB=2，AC=3，D是边BC的中点，则

AD

•

BC

=

 

．

Answer 1

分析：由△ABC中，AB=2，AC=3，D是边BC的中点，我们易将

AD

•

BC

中两个向量变形为：

BC

=

AC

-

AB

，

AD

=

1

2

AC

+

1

2

AB

，然后再利用向量数量积的计算公式，代入即可得到答案．

解答：解：根据向量的加减法法则有：

BC

=

AC

-

AB

AD

=

1

2

AC

+

1

2

AB

，
此时

BC

•

AD

=(

AC

-

AB

)•

1

2

(

AC

+

AB

)
=

1

2

(

AC

2-

AB

2)
=

1

2

(9-4)
=

5

2

故答案为：

5

2

点评：如果两个非量平面向量平行（共线），则它们的方向相同或相反，此时他们的夹角为0或π．当它们同向时，夹角为0，此时向量的数量积，等于他们模的积；当它们反向时，夹角为π，此时向量的数量积，等于他们模的积的相反数．如果两个向量垂直，则它们的夹角为

π

2

，此时向量的数量积，等于0．