题目内容
12.已知函数f(x)=$\frac{{x}^{2}+x+1}{{e}^{x}}$.(1)求函数y=f(x)的单调区间;
(2)若曲线y=f(x)与直线y=b(b∈R)有3个交点,求实数b的取值范围;
(3)过点P(-1,0)可作几条直线与曲线y=f(x)相切?请说明理由.
分析 (1)求导数,利用导数的正负求函数y=f(x)的单调区间;
(2)确定函数的极值,利用曲线y=f(x)与直线y=b(b∈R)有3个交点,求实数b的取值范围;
(3)设切点,求出切线方程,确定切点的个数,即可确定过点P(-1,0)可作几条直线与曲线y=f(x)相切.
解答 解:(1)f′(x)=(x-x2)e-x,
由f′(x)>0,可得0<x<1,f′(x)<0,可得x<0或x>1,
∴函数的单调递增区间是(0,1),单调递减区间是(-∞,0),(1,+∞);
(2)由(1),f(0)=1,f(1)=$\frac{3}{e}$,
∵曲线y=f(x)与直线y=b(b∈R)有3个交点,
∴1<b<$\frac{3}{e}$;
(3)设切点为(m,n),则f′(m)=(m-m2)e-m,
∴切线方程为y-n=(m-m2)e-m(x-m),
代入(-1,0),整理可得m3+m2+1=0,
设g(m)=m3+m2+1,g′(m)=3m2+2m,
由g′(m)>0,可得m$<-\frac{2}{3}$或m>0,g′(m)<0,可得-$\frac{2}{3}$<m<0,
∴函数g(m)的单调递减区间是(-$\frac{2}{3}$,0),单调递增区间是(-∞,-$\frac{2}{3}$),(0,+∞);
∵g(-$\frac{2}{3}$)>0,g(0)>0,
∴g(m)=0有唯一解,
∴过点P(-1,0)可作1条直线与曲线y=f(x)相切.
点评 本题考查函数的导数的综合应用,切线方程的求法,函数的单调性以及函数的最值,考查分析问题解决问题的能力,转化思想的应用,是难度比较大的题目.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
2.在△ABC中,已知$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在边BC上,且$\overrightarrow{BD}$=$3\overrightarrow{DC}$,用$\overrightarrow a$,$\overrightarrow b$表示$\overrightarrow{AD}$,则$\overrightarrow{AD}$=( )
| A. | $\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ | B. | $\frac{3}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$ | D. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{3}{4}$$\overrightarrow{b}$ |
3.已知命题p:?x∈R,使得x2-x+2<0;命题函数f(x)=$\frac{4}{x}$-log3x在区间(3,4)内没有零点.下列命题为真命题的是( )
| A. | (¬p)∧(¬q) | B. | p∧q | C. | (¬p)∧p) | D. | (p)∨q |
7.已知一批10000只白炽灯泡的光通量X~N(200,100),则这批灯泡中光通量X>220个数大约为( )
(参考数据:若X:N(μ,2),则X在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内的概率分别为68.3%,95.4%,99.7% )
(参考数据:若X:N(μ,2),则X在区间(μ-σ,μ+σ),(μ-2σ,μ+2σ),(μ-3σ,μ+3σ)内的概率分别为68.3%,95.4%,99.7% )
| A. | 230 | B. | 460 | C. | 4770 | D. | 9540 |
4.命题“?x0>0,2${\;}^{{x}_{0}}$≤0”的否定是( )
| A. | ?x>0,2x>0 | B. | ?x≤0,2x>0 | C. | ?x>0,2x<0 | D. | ?x≤0,2x<0 |
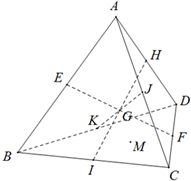 在四面体ABCD中,若E、F、H、I、J、K分别是棱AB、CD、AD、BC、AC、BD的中点,则EF、HI、JK相交于一点G,则点G为四面体ABCD的重心.设A(0,0,2),B(2,0,0),C(0,3,0),D(2,3,2).
在四面体ABCD中,若E、F、H、I、J、K分别是棱AB、CD、AD、BC、AC、BD的中点,则EF、HI、JK相交于一点G,则点G为四面体ABCD的重心.设A(0,0,2),B(2,0,0),C(0,3,0),D(2,3,2).