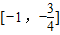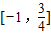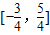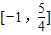题目内容
关于x的方程cosx-lg|x|=0的根的个数( )
| A.1 | B.2 | C.4 | D.6 |
原方程即cosx=lg|x|,在同一坐标系内作出y=cosx与y=lg|x|的图象

由于两个函数均为偶函数,因此方程的根必定为偶数,只须研究当x≥0时的图象
∵x≥0时,cos
=
>lg
,且cosπ=-1<lgπ
∴在区间[0,π]上,两个图象有一个交点
又∵当x∈(π,3π)时,lgx∈(0,1),
而cosx在(π,2π)上为增函数,在(2π,3π)上为减函数,最大值为1
∴在区间(π,3π)上,两个图象有两个交点
而当x≥3π时,易得在[3π,10]上两个图象没有交点
由于在区间(10,+∞)上,lgx>1恒成立而cosx≤1,两个图象也没有交点
∴两图象在x≥3π时没有交点.
综上所述,当x≥0时,y=cosx与y=lg|x|的有3交点,得cosx=lg|x|有三个不同的根
结合两个函数均为偶函数,得当x<0时,cosx=lg|x|也有三个不同的根,故方程cosx-lg|x|=0的根的个数为6
故选:D

由于两个函数均为偶函数,因此方程的根必定为偶数,只须研究当x≥0时的图象
∵x≥0时,cos
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
∴在区间[0,π]上,两个图象有一个交点
又∵当x∈(π,3π)时,lgx∈(0,1),
而cosx在(π,2π)上为增函数,在(2π,3π)上为减函数,最大值为1
∴在区间(π,3π)上,两个图象有两个交点
而当x≥3π时,易得在[3π,10]上两个图象没有交点
由于在区间(10,+∞)上,lgx>1恒成立而cosx≤1,两个图象也没有交点
∴两图象在x≥3π时没有交点.
综上所述,当x≥0时,y=cosx与y=lg|x|的有3交点,得cosx=lg|x|有三个不同的根
结合两个函数均为偶函数,得当x<0时,cosx=lg|x|也有三个不同的根,故方程cosx-lg|x|=0的根的个数为6
故选:D

练习册系列答案
相关题目
若关于x的方程cosx+sin2x+m-
=0恒有实数解,则实数m的取值范围是( )
| 1 |
| 4 |
A、[-1,-
| ||||
B、[-1,
| ||||
C、[-
| ||||
D、[-1,
|
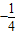 =0恒有实数解,则实数m的取值范围是( )
=0恒有实数解,则实数m的取值范围是( )