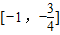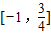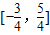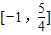题目内容
关于x的方程cosx-sinx+a=0在区间[0，π]上有解，则实数a的取值范围是 ．
【答案】分析：由cosx-sinx+a=0在区间[0，π]上有解，即a=sinx-cosx=
在[0，π]上有解，由0≤x≤π 可得
，从而可求a的范围
解答：解：cosx-sinx+a=0在区间[0，π]上有解
即a=sinx-cosx=
在[0，π]上有解
∵0≤x≤π∴
∴
∴
∴
故答案为：
点评：本题主要考查了方程的解的存在，函数中含有参数时，分类参数a，通过辅助角公式及三角函数的性质求解三角函数的范围，进而可求a的范围
在[0，π]上有解，由0≤x≤π 可得，从而可求a的范围解答：解：cosx-sinx+a=0在区间[0，π]上有解
即a=sinx-cosx=
在[0，π]上有解∵0≤x≤π∴
∴
∴
∴
故答案为：
点评：本题主要考查了方程的解的存在，函数中含有参数时，分类参数a，通过辅助角公式及三角函数的性质求解三角函数的范围，进而可求a的范围
练习册系列答案
相关题目
若关于x的方程cosx+sin2x+m-
=0恒有实数解，则实数m的取值范围是（ ）
| 1 |
| 4 |
A、[-1，-
| ||||
B、[-1，
| ||||
C、[-
| ||||
D、[-1，
|
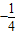=0恒有实数解，则实数m的取值范围是（ ）
