题目内容
一首项为正数的等差数列{an}中,S5=S13,试问:这个数列前多少项和最大?
思路解析:利用等差数列前n项和公式求出Sn的函数表达式,再求该函数的最大值. 解法一:∵S5=S13,∴5a1+ 整理,得d=- 于是Sn=na1+ ∴a1>0,- ∴当n=- 解法二:由等差数列前n项和Sn=an2+bn知,Sn是关于n的二次函数,且S5=S13,故二次函数图象的对称轴为n= 解法三:令Sn=an2+bn,由S5=S13得 25a+5b=169a+13b,∴b+18a=0,b=-18a, 又a1=S1=a+b>0,∴-18a+a>0,a<0, 故Sn=an2-18an, 而a<0,所以当n=--18a2·a=9时,Sn最大. 解法四:∵a1>0,d<0,∴Sn有最大值. 若前n项和最大,则应有 故n=9时,Sn最大. 解法五:由S5=S13知5a1+ 即a1+8d+a1+9d=0,也就是a9+a10=0. ∵a1>0,d<0,∴a9>0,a10<0,所以S9最大. 深化升华 (1)以上五种解法,前三种都属于求函数Sn的最大值,只不过运用了三种不同的求最值的方法;后二种各有新意,思维独到,应仔细品味. (2)当等差数列的公差d<0时,数列是递减数列,若前n项都是正值,则其前n项和有最大值;当等差数列的公差d>0时,数列是递增数列,若前n项都是负值,则其前n项和有最小值.![]() ×d=13a1+
×d=13a1+![]() ×d.
×d.![]() a1,而a1>0,则d<0.
a1,而a1>0,则d<0.![]() d=na1+
d=na1+![]() ×(-
×(-![]() a1)=-
a1)=-![]() n.
n.![]() <0,
<0,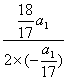 =9时,Sn取得最大值.
=9时,Sn取得最大值.![]() =9,故当n=9时,Sn取最大值.
=9,故当n=9时,Sn取最大值.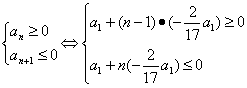
![]() 8.5≤n≤9.5.
8.5≤n≤9.5.![]() ×d=13a1+
×d=13a1+![]() ×d,整理得2a1+17d=0,
×d,整理得2a1+17d=0,
小学生家庭作业系列答案
考易通课时全优练系列答案
与名师对话同步单元测试卷系列答案
黄冈状元笔记系列答案
练习册吉林教育出版集团有限责任公司系列答案
练习册湖北教育出版社系列答案
新课标同步练习系列答案
实验作业系列答案
组合训练湖北教育出版社系列答案
伴你快乐成长开心作业系列答案
| A、4009 | B、4010 | C、4011 | D、4012 |
 已知a2010与a2011是首项为正数的等差数列{an}相邻的两项,且函数y=(x-a2010)(x-a2011)的图象如图所示,则使前n项和Sn>0成立的最大自然数n是( )
已知a2010与a2011是首项为正数的等差数列{an}相邻的两项,且函数y=(x-a2010)(x-a2011)的图象如图所示,则使前n项和Sn>0成立的最大自然数n是( )