题目内容
设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{
解:设等差数列{an}的公差为d,则Sn=na1+![]() n(n-1)d.∵S7=7,S15=75,
n(n-1)d.∵S7=7,S15=75,
∴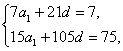
即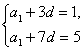
解得a1=-2,d=1.
∴![]() =a1+
=a1+![]() (n-1)d=-2+
(n-1)d=-2+![]() (n-1)=
(n-1)=![]() .
.
∴![]() -
-![]() =
=![]() .
.
∴数列{![]() }是等差数列,其首项为-2,公差为
}是等差数列,其首项为-2,公差为![]() .
.
∴Tn=![]() n2-
n2-![]() n.
n.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{
解:设等差数列{an}的公差为d,则Sn=na1+![]() n(n-1)d.∵S7=7,S15=75,
n(n-1)d.∵S7=7,S15=75,
∴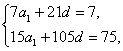
即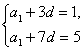
解得a1=-2,d=1.
∴![]() =a1+
=a1+![]() (n-1)d=-2+
(n-1)d=-2+![]() (n-1)=
(n-1)=![]() .
.
∴![]() -
-![]() =
=![]() .
.
∴数列{![]() }是等差数列,其首项为-2,公差为
}是等差数列,其首项为-2,公差为![]() .
.
∴Tn=![]() n2-
n2-![]() n.
n.

 阅读快车系列答案
阅读快车系列答案