题目内容
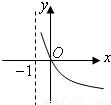
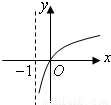
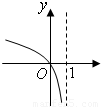
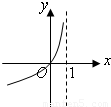
函数y=kax-a-x（a＞0，a≠1）是奇函数又是减函数，则y=-loga（k-x）的大致图象是（ ）
分析：根据已知中函数y=kax-a-x（a＞0，a≠1）是奇函数，根据定义在R上的奇函数图象必过原点，可得k=1，再由函数y=kax-a-x（a＞0，a≠1）是减函数，结合指数函数的单调性及函数单调性的性质，可得0＜a＜1，进而分析出函数y=-loga（k-x）=-loga（1-x）的定义域，单调性，即可得到答案．
解答：解：∵函数y=kax-a-x（a＞0，a≠1）是奇函数
∴函数的图象必要原点
故k=1
又∵函数y=kax-a-x（a＞0，a≠1）是减函数，
故0＜a＜1
故函数y=-loga（k-x）=-loga（1-x）的定义域为（-∞，1），可排除A，B
且在区间（-∞，1）上为减函数，且过（0，0）点，可排除D
故选C
∴函数的图象必要原点
故k=1
又∵函数y=kax-a-x（a＞0，a≠1）是减函数，
故0＜a＜1
故函数y=-loga（k-x）=-loga（1-x）的定义域为（-∞，1），可排除A，B
且在区间（-∞，1）上为减函数，且过（0，0）点，可排除D
故选C
点评：本题考查的知识点是函数的图象，函数的单调性的性质，函数的奇偶性的性质，其中根据已知条件，结合奇函数的性质及函数单调性的性质，判断出参数a的范围及k的值，是解答本题的关键．
练习册系列答案
相关题目
下列函数关系中，可以看着是指数型函数y=kax（k∈R，a＞0且a≠1）模型的是（ ）
| A、竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）． | B、我国人口年自然增长率为1%，这样我国人口总数随年份的变化关系． | C、如果某人ts内骑车行进了1km，那么此人骑车的平均速度v与时间t的函数关系． | D、信件的邮资与其重量间的函数关系． |
