题目内容

已知-
π
2
＜α＜
π
2
，-
π
2
＜β＜
π
2
，且tanα，tanβ是方程x2+6x+7=0的两个根，求α+β的值．
∵tanα+tanβ=-6，tanα•tanβ=7（4分）
∵tan(α+β)=
tanα+tanβ
1-tanα•tanβ
=
-6
1-7
=1（8分）
∴tanα＜0，tanβ＜0
∴-
π
2
＜α＜0，-
π
2
＜β＜0（12分）
∴-π＜α+β＜0，
∴α+β=-
3π
4
（14分）
练习册系列答案
相关题目
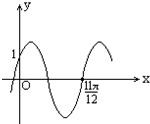
已知如图是函数y=2sin（ωx+φ）（|φ|＜
π
2
）的图象，那么（　　）
精英家教网
A、?=
10
11
，φ=
π
6
B、?=
10
11
，φ=-
π
6
C、?=2，φ=
π
6
D、?=2，φ=-
π
6
已知α∈(
π
2
，π)，且sin（π-α)+cos(2π+α)=
2
3
+cos（2π+α）=
2
3

求证：（1）sinα-cosα；
（2）tanα；
（3）sin3(
3π
2
-a)+cos3（
π
2
-α)的值．
已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是
④
④
．?
已知函数f（x）=ln（x-1）-k（x-1）+1（k∈R）．
（1）若k=2，求以M（2，f（2））为切点的曲线的切线方程；
（2）若函数f（x）≤0恒成立，确定实数K的取值范围；
（3）证明：
ln2
3
+
ln3
4
+
ln4
5
+…+
lnn
n+1
＜
(n-1)2
n+1
．

已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是________．?

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网