题目内容
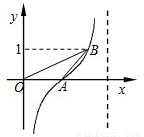
函数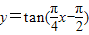 的部分图象如图所示,则
的部分图象如图所示,则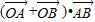 =( )
=( )
A.4
B.6
C.1
D.2
【答案】分析:先利用正切函数求出A,B两点的坐标,进而求出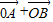 与
与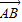 的坐标,再代入平面向量数量积的运算公式即可求解.
的坐标,再代入平面向量数量积的运算公式即可求解.
解答:解:因为y=tan(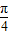 x-
x-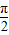 )=0⇒
)=0⇒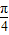 x-
x-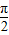 =kπ⇒x=4k+2,由图得x=2;故A(2,0)
=kπ⇒x=4k+2,由图得x=2;故A(2,0)
由y=tan(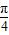 x
x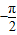 )=1⇒
)=1⇒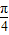 x-
x-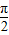 =k
=k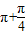 ⇒x=4k+3,由图得x=3,故B(3,1)
⇒x=4k+3,由图得x=3,故B(3,1)
所以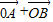 =(5,1),
=(5,1),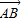 =(1,1).
=(1,1).
∴(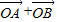 )
)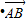 =5×1+1×1=6.
=5×1+1×1=6.
故选 B.
点评:本题主要考查平面向量数量积的运算,考查的是基础知识,属于基础题.解决本题的关键在于利用正切函数求出A,B两点的坐标.
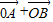 与
与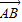 的坐标,再代入平面向量数量积的运算公式即可求解.
的坐标,再代入平面向量数量积的运算公式即可求解.解答:解:因为y=tan(
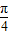 x-
x-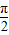 )=0⇒
)=0⇒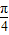 x-
x-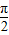 =kπ⇒x=4k+2,由图得x=2;故A(2,0)
=kπ⇒x=4k+2,由图得x=2;故A(2,0)由y=tan(
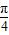 x
x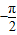 )=1⇒
)=1⇒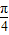 x-
x-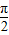 =k
=k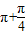 ⇒x=4k+3,由图得x=3,故B(3,1)
⇒x=4k+3,由图得x=3,故B(3,1)所以
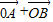 =(5,1),
=(5,1),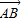 =(1,1).
=(1,1).∴(
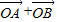 )
)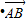 =5×1+1×1=6.
=5×1+1×1=6.故选 B.
点评:本题主要考查平面向量数量积的运算,考查的是基础知识,属于基础题.解决本题的关键在于利用正切函数求出A,B两点的坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长为2的等边三角形,则f(1)的值为( ) 已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( )
已知函数f(x)是(-∞,0)∪(0,+∞)上的奇函数,且当x<0时,函数的部分图象如图所示,则不等式xf(x)<0的解集是( ) (2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4
(2012•福州模拟)函数f(x)=2cos(ωx+φ)(ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,点A、B分别为该部分图象的最高点与最低点,且这两点间的距离为4 (2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( )
(2012•江西模拟)已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函数,该函数的部分图象如图所示,△EFG是边长1为的等边三角形,则f(1)的值为( ) 函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且
函数y=sin(ωx+?)(ω>0,0<?<π)为偶函数,该函数的部分图象如图所示,A、B分别为最高点与最低点,并且