题目内容
 如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=
如图,在平面直角坐标系xOy中,椭圆C的中心在坐标原点O,右焦点为F.若C的右准线l的方程为x=4,离心率e=
| ||
| 2 |
(1)求椭圆C的标准方程;
(2)设点P为直线l上一动点,且在x轴上方.圆M经过O、F、P三点,求当圆心M到x轴的距离最小时圆M的方程.
分析:(1)设椭圆C的标准方程是
+
=1(a>0,b>0),由题意知
,由此能够求出椭圆C的方程.
(2)由(1)知,F(2,0),由题意设P(4,t),t>0,线段OF的垂直平分线方程为x=1,因为线段FP的中心为(3,
),斜率为
.所以线段FP的垂直平分线方程为y-
=-
(x-3),由此入手能够求出圆M的方程.
| x2 |
| a2 |
| y2 |
| b2 |
|
(2)由(1)知,F(2,0),由题意设P(4,t),t>0,线段OF的垂直平分线方程为x=1,因为线段FP的中心为(3,
| t |
| 2 |
| t |
| 2 |
| t |
| 2 |
| 2 |
| t |
解答:解:(1)由题意,设椭圆C的标准方程是
+
=1(a>0,b>0),
则
,
解得a=2
,b=2,c=2,
∴所求椭圆C的方程为
+
=1.
(2)由(1)知,F(2,0),由题意设P(4,t),t>0,
线段OF的垂直平分线方程为x=1,①
因为线段FP的中心为(3,
),斜率为
.
所以线段FP的垂直平分线方程为y-
=-
(x-3),
即y=-
x+
+
,②
联立①②,解得
,
即:圆心M(1,
+
),
∵t>0,∴
+
≥2
=2
,
当且仅当
=
,即t=2
时,
圆心M到x轴的距离最小,此时圆心为M(1,2
),半径为OM=3,
故所求圆M的方程为(x-1)2+(y-2
)2=9.
| x2 |
| a2 |
| y2 |
| b2 |
则
|
解得a=2
| 2 |
∴所求椭圆C的方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)由(1)知,F(2,0),由题意设P(4,t),t>0,
线段OF的垂直平分线方程为x=1,①
因为线段FP的中心为(3,
| t |
| 2 |
| t |
| 2 |
所以线段FP的垂直平分线方程为y-
| t |
| 2 |
| 2 |
| t |
即y=-
| 2 |
| t |
| 5 |
| t |
| t |
| 2 |
联立①②,解得
|
即:圆心M(1,
| t |
| 2 |
| 4 |
| t |
∵t>0,∴
| t |
| 2 |
| 4 |
| t |
|
| 2 |
当且仅当
| t |
| 2 |
| 4 |
| t |
| 2 |
圆心M到x轴的距离最小,此时圆心为M(1,2
| 2 |
故所求圆M的方程为(x-1)2+(y-2
| 2 |
点评:本题考查椭圆标准方程的求法和求当圆心M到x轴的距离最小时圆M的方程.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
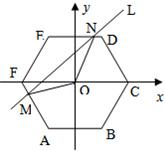 如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )
如图,在直角坐标平面内有一个边长为a、中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为( )| A、偶函数 | B、奇函数 | C、不是奇函数,也不是偶函数 | D、奇偶性与k有关 |
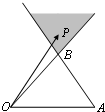 如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且
如图,在△OAB中,点P是线段OB及线段AB延长线所围成的阴影区域(含边界)的任意一点,且 1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
1、如图,在直角坐标平面内有一个边长为a,中心在原点O的正六边形ABCDEF,AB∥Ox.直线L:y=kx+t(k为常数)与正六边形交于M、N两点,记△OMN的面积为S,则函数S=f(t)的奇偶性为
 (2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是
(2008•海珠区一模)如图,在直角坐标平面内,射线OT落在60°的终边上,任作一条射线OA,OA落在∠xOT内的概率是