Question

如图,有公共边AB的两个全等的矩形ABCD和ABEF不共面,对角线AC和BF上各有点M和N,且AM=FN.连结MN.求证:MN∥平面BCE.

Answer 1

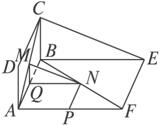
证法一:要证MN∥平面BCE,考虑到“若两个平面平行,则在其中一个平面内的任一条直线必平行于另一个平面”,可过MN作一个平面,证其与平面BCE平行.若过M作MQ∥CB,连结QN,如图(1),则平面MNQ平行于平面BCE.

如图(1),∵ABCD和ABEF是有公共边AB的全等的两个矩形,

              (1)

∴对角线AC=FB.

∵AM=FN,

∴MC=NB.

过M作MQ∥CB,交AB于Q,连结QN,则.

∴QN∥AF.

∵AF∥BE,

∴QN∥BE.

又MQ∥CB且MQ与QN相交,

∴平面MNQ∥平面BCE.

∴MN∥平面BCE.

证法二:如证法一所述,为证MN∥平面BCE,需寻求过MN且平行于平面BCE的平面.如图(2),可过N作NQ∥BE,连结MQ.在证MQ∥CB时,若不像证法一利用比例关系,还可考虑由证MQ⊥AB得到.为利用题设条件,可过N作NP⊥AF于P,只需证△AMQ≌△NFP,则有∠AQM=∠NPF=90°,即MQ⊥AB.

              (2)

如图(2),过N作NQ∥BE,交AB于Q.连结MQ.又过N作NP⊥AF于P,则NP∥AB,且AQ=PN.

∵ABCD和ABEF为有公共边AB的全等矩形,∴BC=AF,AB=AB.

∴Rt△ABC≌Rt△ABF.

从而∠CAB=∠ABF=∠PNF.

又AM=FN,AQ=PN,

∴△AMQ≌△NFP.

∴∠AQM=∠NPF=90°,即MQ⊥AB.

∵CB⊥AB,∴MQ∥CB.

又NQ∥BE,且MQ与NQ相交,

∴平面MNQ∥平面BCE.

∴MN∥平面BCE.

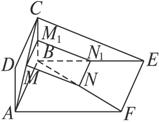
证法三:考虑到直线与平面平行的判定定理,需在平面BCE内找一条直线,使其与MN平行.可作MM₁⊥BC于M₁,作NN₁⊥BE于N₁,连结M₁N₁,证明MM₁NN₁,即易得MN∥M₁N₁.

如图(3),过M作MM₁⊥BC于M₁,过N作NN₁⊥BE于N₁,连结M₁N₁,则MM₁∥AB,NN₁∥AB.

              (3)

∴MM₁∥NN₁.

∵ABCD和ABEF为有公共边AB的全等矩形,且AM=FN,∴CA=BF,CM=BN.由,

得MM₁=NN₁.

∴MNN₁M₁为平行四边形.∴MN∥M₁N₁.

故MN∥平面BCE.

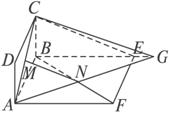
证法四:如证法三所述,要证MN∥平面BCE,需在平面BCE内找一条直线与MN平行.如图(4),若连结AN并延长与BE的延长线交于G,假设已有MN∥平面BCE,则在△ACG中MN应该平行于CG.

               (4)

故可设法由其他途径证MN∥CG.

如图(4),连结AN并延长与BE的延长线交于点G.连结CG.

∵ABCD与ABEF是有公共边AB的全等矩形,且AM=FN,∴AC=BF,MC=NB.

∵AF∥BG,∴.

于是MN∥CG.故MN∥平面BCE.

小结:在证MN∥平面BCE时,证法一和证法二用的是两平行平面的性质,所以必须构造过MN且能与平面BCE平行的平面;证法三和证法四用的是直线和平面平行的判定定理,所以必须在平面BCE内找一条与MN平行的直线.证题方向明确,就不至于在作辅助线和证题时盲目行动.证法一由于用了比例线段关系,因此较简洁;证法四作出△ACG,再运用成比例线段的关系,证明更简洁.可见,恰当地添作辅助线,对迅速、顺利地证题起着重要的作用.