题目内容
【题目】[选修4-5:不等式选讲]
已知函数![]() .
.
(1)解不等式:![]() ;
;
(2)对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)解法一:写出分段函数![]() 的解析式,讨论
的解析式,讨论![]() 的范围,求出分段函数不同自变量范围的不等式的解,再求这些解的并集即可.
的范围,求出分段函数不同自变量范围的不等式的解,再求这些解的并集即可.
解法二:写出分段函数![]() 的解析式,绘制函数图象,计算函数
的解析式,绘制函数图象,计算函数![]() 与
与![]() 的交点坐标,根据函数图象确定不等式的解.
的交点坐标,根据函数图象确定不等式的解.
解法三:根据绝对值在数轴上的几何意义,确定不等式的解.
(2)将![]() 恒成立问题转化成
恒成立问题转化成![]() 问题,确定
问题,确定![]() 后,解关于
后,解关于![]() 的一元二次不等式,即可求出实数
的一元二次不等式,即可求出实数![]() 的取值范围.
的取值范围.
解法一:根据三角不等式,确定函数最小值
解法二:根据函数图象,确定函数最小值.
详解:(1)解法一: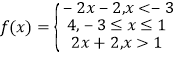
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ,
,
所以不等式![]() 的解集为
的解集为![]() ;
;
(1)解法二:
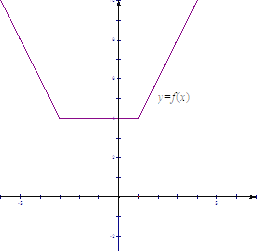
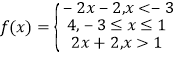 ,两个函数的图象如图所示:
,两个函数的图象如图所示:
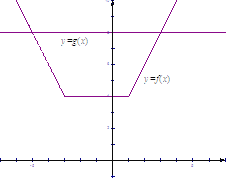
由图像可知,两函数图象的交点为
![]() 和
和![]() ,
,
所以不等式![]() 即
即![]() 的解集为
的解集为![]()
(注:如果作出函数![]() 的图象,写出
的图象,写出![]() 的解集,可参照解法2的标准给分)
的解集,可参照解法2的标准给分)
解法三:如图,

设数轴上与![]() 对应的点分别是
对应的点分别是![]() ,那么
,那么![]() 两点的距离是4,因此区间
两点的距离是4,因此区间![]() 上的数都是原不等式的解。
上的数都是原不等式的解。
先在数轴上找出与点![]() 的距离之和为
的距离之和为![]() 的点,将点
的点,将点![]() 向左移动2个单位到点
向左移动2个单位到点![]() ,这时有
,这时有![]() ,
,
同理,将点![]() 向右移动2个单位到点
向右移动2个单位到点![]() ,这时也有
,这时也有![]() ,
,
从数轴上可以看到,点![]() 与
与![]() 之间的任何点到点
之间的任何点到点![]() 的距离之和都小于8, 点
的距离之和都小于8, 点![]() 的左边或点
的左边或点![]() 的右边的任何点到点
的右边的任何点到点![]() 的距离之和都大于8,
的距离之和都大于8,
所以,原不等式的解集是![]()
(2)解法一:![]() ,
,
当![]() 时“
时“![]() ”成立,
”成立,
又![]() 任意
任意![]() ,
,![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.
解法二: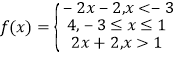
作函数![]() 的图象如图:
的图象如图:
由图象可知,函数![]() 的最小值为4,
的最小值为4,
(注:如果第(1)问用解法2,可直接由(1)得最小值为4,不必重复说明)
又![]() 任意
任意![]() ,
,![]() 恒成立,
恒成立,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,
∴![]() 的取值范围为
的取值范围为![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.