题目内容
4.已知正方体ABCD-A1B1C1D1两顶点的坐标为B(-1,2,-1),D1(3,-2,3),则此正方体的外接球的表面积等于48π.分析 正方体的外接球的直径就是正方体的体对角线的长,求出正方体的对角线长,可求球的表面积:
解答 解:因为正方体ABCD-A1B1C1D1两顶点的坐标为B(-1,2,-1),D1(3,-2,3),
所以球的直径为:BD1=$\sqrt{(3+1)^{2}+(-2-2)^{2}+(3+1)^{2}}$=4$\sqrt{3}$,
所以球的半径是2$\sqrt{3}$,球的表面积:4π•12=48π
故答案为:48π.
点评 本题考查球的内接体,多面体的外接球,球的表面积知识,考查计算能力,是基础题.

练习册系列答案
相关题目
15.已知命题p:?m∈R,使得函数f(x)=x2+(m-1)x2-2是奇函数,命题q:向量$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是:“$\overrightarrow{a}$$∥\overrightarrow{b}$”的充要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧q | C. | p∧(¬q) | D. | (¬p)∧(¬q) |
19.复数i-i2在复平面内表示的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.若${(x+\frac{a}{{\root{3}{x}}})^8}$(a>0)的展开式中当且仅当第6项系数最大,则实数a的取值范围是( )
| A. | $\frac{5}{4}<a<2$ | B. | $\frac{5}{4}≤a≤2$ | C. | $2≤a≤\frac{7}{2}$ | D. | $2<a<\frac{7}{2}$ |
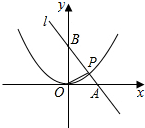 如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.
如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内交于P点,如果△AOP的面积为2,求此抛物线的解析式.