题目内容
16.已知函数f(x)=$\frac{1-2x}{x+1}$(x≥1),数列an=f(n)(n∈N*),证明:数列{an}是递减数列.分析 先证明函数f(x)=$\frac{3}{1+x}$-2在x≥1时单调递减,即可证明数列{an}是递减数列.
解答 证明:∵函数f(x)=$\frac{1-2x}{x+1}$=$\frac{3-2(1+x)}{1+x}$=$\frac{3}{1+x}$-2(x≥1),
由函数y=$\frac{3}{1+x}$在x≥1时单调递减,可知:x≥1时,函数f(x)单调递减,
因此数列an=f(n)=$\frac{3}{1+n}-2$(n∈N*),也单调递减.
点评 本题考查了数列的通项公式、函数的单调性与数列的单调性的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
4.设函数f(x)=sin(2x+α)+$\sqrt{3}$cos(2x+α)(0<α<$\frac{π}{2}$),且图象关于直线x=$\frac{π}{24}$对称,则( )
| A. | 函数f(x)的周期为π,且在区间[$\frac{π}{3}$,π]内单调递增 | |
| B. | 函数f(x)的周期为π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| C. | 函数f(x)的周期为2π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| D. | 函数f(x)的周期为$\frac{π}{2}$,且在区间[$\frac{π}{2}$,π]内单调递增 |
11.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与对称轴垂直的直线与渐近线交于A,B两点,若△OAB的面积为$\frac{\sqrt{13}bc}{3}$,则双曲线的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{\sqrt{13}}{2}$ | D. | $\frac{\sqrt{13}}{3}$ |
1.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点是F,左、右顶点分别是A1,A2,过F做直线A1A2的垂线与双曲线交于B,C两点,若A1B⊥A2C,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{2}$ |
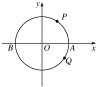 如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.
如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.