题目内容
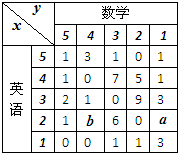下表为某班英语及数学成绩的分布．学生共有50人，成绩分1～5五个档次．例如表中所示英语成绩为4分、数学成绩为2分的学生为5人．将全班学生的姓名卡片混在一起，任取一枚，该卡片同学的英语成绩为x，数学成绩为y（注：没有相同姓名的学生）．（Ⅰ）求a+b的值；
（Ⅱ）求x=1的概率；
（Ⅲ）求x≥3且y=3的概率．
分析：（I）根据共有学生50人，分成5个档次，得到每个档次有10人．根据已经写出的几个部分，得到结果．
（II）本题是一个等可能事件的概率，试验发生包含的事件数是50，满足条件的事件是1+3+1，得到概率．
（III）本题是一个等可能事件的概率，试验发生包含的事件数是50，满足条件的事件数是8，得到概率．
（II）本题是一个等可能事件的概率，试验发生包含的事件数是50，满足条件的事件是1+3+1，得到概率．
（III）本题是一个等可能事件的概率，试验发生包含的事件数是50，满足条件的事件数是8，得到概率．
解答：解：（I）∵学生共有50人，成绩分1～5五个档次
∴每个档次有10人，
∴a+b=10-7=3；
（II）由题意知本题是一个等可能事件的概率，
试验发生包含的事件数是50，
满足条件的事件是1+3+1
∴P(x=1)=
=
；
（III）由题意知本题是一个等可能事件的概率，
试验发生包含的事件数是50，
满足条件的事件数是8，
∴P(x≥3，y=3)=
=
．
∴每个档次有10人，
∴a+b=10-7=3；
（II）由题意知本题是一个等可能事件的概率，
试验发生包含的事件数是50，
满足条件的事件是1+3+1
∴P(x=1)=
| 1+3+1 |
| 50 |
| 1 |
| 10 |
（III）由题意知本题是一个等可能事件的概率，
试验发生包含的事件数是50，
满足条件的事件数是8，
∴P(x≥3，y=3)=
| 8 |
| 50 |
| 4 |
| 25 |
点评：本题考查等可能事件的概率，本题解题的关键是正确理解图形，注意分析图形中所给的隐含已知条件，本题是一个基础题．
练习册系列答案
相关题目
下表为某班英语及数学成绩公布，全班共有学生50人，成绩分为1～5五个档次，设x，y分别表示英语成绩和数学成绩，例如表中英语成绩为5分的共6人，数学成绩为3分的共有15人．
（1）x=4的概率是多少？x=4且y=3的概率是多少？
（2）在x≥3的基础上，y=3同时成立的概率是多少？
（3）x=2的概率是多少？a+b的值是多少？
（1）x=4的概率是多少？x=4且y=3的概率是多少？
（2）在x≥3的基础上，y=3同时成立的概率是多少？
（3）x=2的概率是多少？a+b的值是多少？
| x分 | 5 | 4 | 3 | 2 | 1 | |
| Y分 | 人数 | |||||
| 5 | 1 | 3 | 1 | 0 | 1 | |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | b | 6 | 0 | a | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
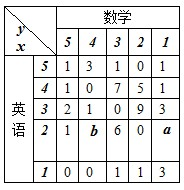下表为某班英语及数学成绩的分布．学生共有50人，成绩分1～5五个档次．例如表中所示英语成绩为4分、数学成绩为2分的学生为5人．将全班学生的姓名卡片混在一起，任取一枚，该卡片同学的英语成绩为x，数学成绩为y．设x，y为随机变量（注：没有相同姓名的学生）