题目内容
下表为某班英语及数学的成绩分布,全班共有学生50人,成绩依次分为A~E共5个等级(A最好,E最差),例如表中所示英语成绩为B,数学成绩为D的学生共5人,设x、y分别表示英语成绩和数学成绩.
(1)x=E的概率是多少?x≥C(即成绩在C或者C以上)的概率是多少?
(2)a+b的值是多少?在所有的x<C的同学中,y=C的概率是多少?
分析:(1)由已知可得,班共有学生50人,x=E的人数有5个,代入等可能事件的概率公式求解即可
x≥C的情况有①x=C②x=B③x=A,且①②③的事件互斥,用互斥事件概率的加法公式求解
(2)结合(1)可求x≥C的人数5,进而可求x<C的同学,从而可求a+b;观察统计图表可得所有的x<C的15名同学中,y=C的有7人,代入等可能事件的概率公式求解即可
x≥C的情况有①x=C②x=B③x=A,且①②③的事件互斥,用互斥事件概率的加法公式求解
(2)结合(1)可求x≥C的人数5,进而可求x<C的同学,从而可求a+b;观察统计图表可得所有的x<C的15名同学中,y=C的有7人,代入等可能事件的概率公式求解即可
解答:解:(1)P(x=E)=
=
;(3分)
P(x≥C)=P(x=C)+P(x=B)+P(x=A)=
;(6分)
(2)由(1)P(x<C)=1-P(x≥C)=
所以x<C的同学有15人,则a+b=3.(9分)
在所有的x<C的15名同学中,y=C的有7人.
所以:在所有的x<C的同学中,P(y=C)=
(12分)
| 1+1+3 |
| 50 |
| 1 |
| 10 |
P(x≥C)=P(x=C)+P(x=B)+P(x=A)=
| 7 |
| 10 |
(2)由(1)P(x<C)=1-P(x≥C)=
| 3 |
| 10 |
所以x<C的同学有15人,则a+b=3.(9分)
在所有的x<C的15名同学中,y=C的有7人.
所以:在所有的x<C的同学中,P(y=C)=
| 7 |
| 15 |
点评:本题考查了由统计图表求解有关数据,等可能事件概率(古典概率)的求解,及在求解概率时,若时间的结果不只一种时,要把基本事件分解几个互斥事件,当事件的正面结果较多或不易求解时,常考虑用对立事件的概率求解.

练习册系列答案
相关题目
下表为某班英语及数学成绩公布,全班共有学生50人,成绩分为1~5五个档次,设x,y分别表示英语成绩和数学成绩,例如表中英语成绩为5分的共6人,数学成绩为3分的共有15人.
(1)x=4的概率是多少?x=4且y=3的概率是多少?
(2)在x≥3的基础上,y=3同时成立的概率是多少?
(3)x=2的概率是多少?a+b的值是多少?
(1)x=4的概率是多少?x=4且y=3的概率是多少?
(2)在x≥3的基础上,y=3同时成立的概率是多少?
(3)x=2的概率是多少?a+b的值是多少?
| x分 | 5 | 4 | 3 | 2 | 1 | |
| Y分 | 人数 | |||||
| 5 | 1 | 3 | 1 | 0 | 1 | |
| 4 | 1 | 0 | 7 | 5 | 1 | |
| 3 | 2 | 1 | 0 | 9 | 3 | |
| 2 | 1 | b | 6 | 0 | a | |
| 1 | 0 | 0 | 1 | 1 | 3 | |
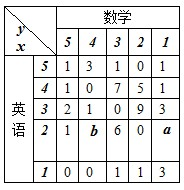 下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为x,数学成绩为y.设x,y为随机变量(注:没有相同姓名的学生)
下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为x,数学成绩为y.设x,y为随机变量(注:没有相同姓名的学生)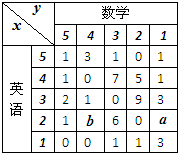 下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为x,数学成绩为y(注:没有相同姓名的学生).
下表为某班英语及数学成绩的分布.学生共有50人,成绩分1~5五个档次.例如表中所示英语成绩为4分、数学成绩为2分的学生为5人.将全班学生的姓名卡片混在一起,任取一枚,该卡片同学的英语成绩为x,数学成绩为y(注:没有相同姓名的学生).