题目内容
直线l过抛物线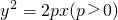 的焦点F,且交抛物线于P、Q两点,由P、Q分别向准线引垂线PR、QS,垂足分别为R、S,如果|PF|=a,|QF|=b,M为RS的中点,则|MF|=________.
的焦点F,且交抛物线于P、Q两点,由P、Q分别向准线引垂线PR、QS,垂足分别为R、S,如果|PF|=a,|QF|=b,M为RS的中点,则|MF|=________.

分析:由题意,取PQ的中点N,利用
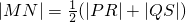 ,根据抛物线定义,可得
,根据抛物线定义,可得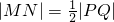 ,所以PM⊥QM,利用△PRM≌△PFM,可得 MF⊥PQ,在Rt△PMQ中,MF⊥PQ,利用射影定理可得结论.
,所以PM⊥QM,利用△PRM≌△PFM,可得 MF⊥PQ,在Rt△PMQ中,MF⊥PQ,利用射影定理可得结论.解答:由题意,取PQ的中点N,
∵M为RS的中点,∴MN是梯形的中位线
∴
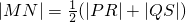
根据抛物线定义,可得|PR|=|PF|=a,|QS|=|QF|=b,
∴
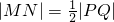 ,∴PM⊥QM.
,∴PM⊥QM.∵PR=PF,∠RPM=∠FPM,PM=PM,∴△PRM≌△PFM,∴∠PFM=∠PRM=90°,∴MF⊥PQ.
在Rt△PMQ中,MF⊥PQ,∴|MF|2=|PF|×|QF|,∴|MF|=

故答案为:

点评:本题考查抛物线的定义,考查抛物线过焦点的性质,考查射影定理的运用,解题的关键是证明抛物线过焦点的性质,属于中档题.

练习册系列答案
相关题目
直线l与抛物线y2=2px(p>0)交于A(x1,y1),B(x2,y2)两不同点:命题s:y1y2=-p2;命题t:直线l过抛物线的焦点,则s是t的( )
| A、充分不必要条件 | B、必要不充分条件 | C、既不充分也不必要条件 | D、充要条件 |
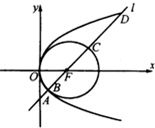 如图,抛物线顶点在原点,圆x2+y2=4x的圆心是抛物线的焦点,直线l过抛物线的焦点,且斜率为2,直线l交抛物线与圆依次为A、B、C、D四点.
如图,抛物线顶点在原点,圆x2+y2=4x的圆心是抛物线的焦点,直线l过抛物线的焦点,且斜率为2,直线l交抛物线与圆依次为A、B、C、D四点.