Question

【题目】已知的定义域为，，使得不等式成立，关于的不等式的解集记为.

（1）若为真，求实数的取值集合；

（2）在（1）的条件下，若是的充分不必要条件，求实数的取值范围.

Answer 1

【答案】（1）；（2）

【解析】

（1）先确定p，q为真的等价条件，若为真则真 真，求交集即可；

（2）利用x∈A”是“x∈B”的充分不必要条件，即AB，确定条件关系，即可求实数m的取值范围．

（1） f（x）的定义域为R，则ax2﹣ax+≥0对任意实数x都成立，

当a＝0时显然满足，当a≠0时，有，解得0＜a≤1．

综上：

，使得不等式成立，∴即a

为真，即真， 真，

（2）①，即，此时

是的充分不必要条件

；

②，即，此时 不符合题意。

③①，即，此时

为的充分不必要条件

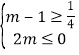无解；

综上所述：