题目内容
命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
C
解析试题分析:全称命题的否定是存在性命题。“对任意的 ”的否定是存在
”的否定是存在 ,选C。
,选C。
考点:复合命题
点评:简单题,涉及命题问题,往往综合性较强,注意运用全称命题的否定是存在性命题。

练习册系列答案
相关题目
若函数 的定义域为
的定义域为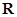 ,那么“
,那么“ ,
, ”是“
”是“ 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知a,b是实数,则“a>0或b>0”是“a+b>0且ab>0”
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题中的假命题是( )
A. | B. |
C. | D. |
下列命题为真命题的是
A.若 为真命题,则 为真命题,则 为真命题 为真命题 |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.命题“若 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
D.命题p: , , ,则 ,则 : : , , |
“1<x<2”是“x<2”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
给定两个命题 ,
, ,若
,若 是
是 的必要而不充分条件,则
的必要而不充分条件,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知集合 ,
, ,则
,则 是
是 的( )
的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
 且
且 ”为假命题,则
”为假命题,则 ”的否命题为“若
”的否命题为“若 ”
” ”的否定是“存在
”的否定是“存在 ”
” ABC中,“
ABC中,“ ”是“
”是“ ”的充要条件
”的充要条件