题目内容
设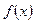 =
=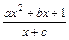 (a>0)为奇函数,且
(a>0)为奇函数,且
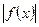 min=
min=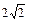 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 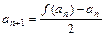 ,
,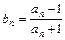 .
.
(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn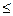
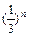 .
.
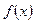 =
=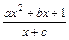 (a>0)为奇函数,且
(a>0)为奇函数,且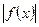 min=
min=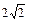 ,数列{an}与{bn}满足 如下关系:a1=2,
,数列{an}与{bn}满足 如下关系:a1=2, 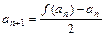 ,
,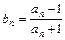 .
.(1)求f(x)的解析表达式;
(2) 证明:当n∈N+时, 有bn
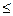
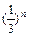 .
.(1)f(x)= 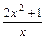 (2 同解析
(2 同解析
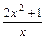 (2 同解析
(2 同解析 由f(x)是奇函数,得 b=c=0,
由|f(x)min|=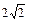 ,得a=2,故f(x)=
,得a=2,故f(x)= 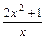
(2)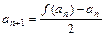 =
=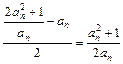 ,
,
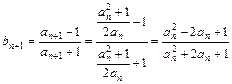 =
=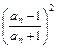 =
=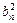
∴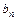 =
=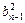 =
=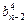 =…=
=…=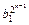 ,而b1=
,而b1=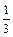
∴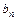 =
=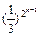
当n=1时, b1=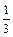 ,命题成立,
,命题成立,
当n≥2时
∵2n-1=(1+1)n-1=1+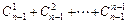 ≥1+
≥1+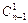 =n
=n
∴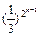 <
<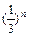 ,即 bn≤
,即 bn≤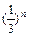 .
.
由|f(x)min|=
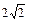 ,得a=2,故f(x)=
,得a=2,故f(x)= 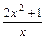
(2)
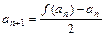 =
=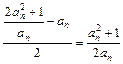 ,
,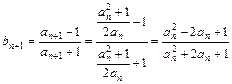 =
=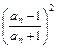 =
=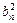
∴
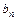 =
=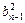 =
=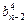 =…=
=…=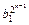 ,而b1=
,而b1=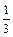
∴
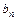 =
=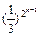
当n=1时, b1=
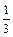 ,命题成立,
,命题成立, 当n≥2时
∵2n-1=(1+1)n-1=1+
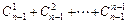 ≥1+
≥1+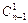 =n
=n∴
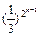 <
<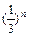 ,即 bn≤
,即 bn≤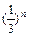 .
. 
练习册系列答案
相关题目
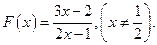
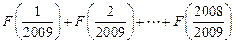 ;
;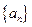 满足
满足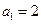 ,
,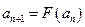 ,求数列
,求数列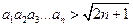 .
.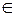
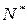 ),其中
),其中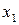 为正实数.
为正实数. 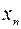 表示xn+1;
表示xn+1;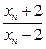 ,证明数列{
,证明数列{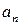 }成等比数列,并求数列{xn}的通项公式;
}成等比数列,并求数列{xn}的通项公式;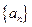 的各项都是正数,
的各项都是正数,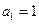 ,
,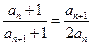 ,
,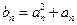 .
.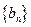 的通项公式;⑵求数列
的通项公式;⑵求数列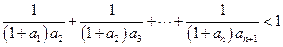 .
.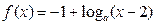 (
(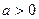 ,且
,且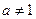 ),
),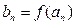 ,
, 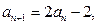 且
且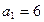 ,
,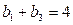
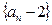 为等比数列
为等比数列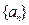 和
和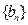 的通项公式。
的通项公式。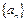 中,
中,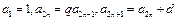 (
(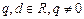 ).
).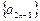 是等比数列,且
是等比数列,且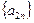 是等差数列,求q, d满足的条件.
是等差数列,求q, d满足的条件.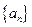 中,
中,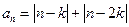 ,若对任意的正整数
,若对任意的正整数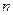 ,
,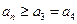 都成立,则
都成立,则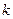 的取值范围为 。
的取值范围为 。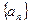 的各项均为正数,它的前n项和Sn满足
的各项均为正数,它的前n项和Sn满足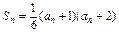 ,并且
,并且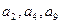 成等比数列.
成等比数列. 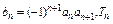 为数列
为数列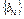 的前n项和,求
的前n项和,求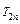 .
.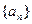 的首项
的首项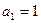 ,公差
,公差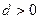 ,且第二项、第五项、第十四项分别是等比数列
,且第二项、第五项、第十四项分别是等比数列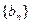 的第二项、第三项、第四项。(1)求数列
的第二项、第三项、第四项。(1)求数列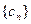 对任意正整数
对任意正整数 均有
均有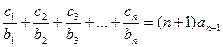 成立,求数列
成立,求数列