题目内容
已知非零向量 、
、 ,满足
,满足 ,则函数
,则函数 (x∈R)是
(x∈R)是
- A.既是奇函数又是偶函数
- B.非奇非偶函数
- C.奇函数
- D.偶函数
D
分析:由已知可得, =
= ,然后结合函数的奇偶性即可检验
,然后结合函数的奇偶性即可检验
解答:∵ ,
,
∴ =
=
=
∴f(-x)= =f(x)
=f(x)
∴f(x)是偶函数
故选D
点评:本题主要考查了向量的数量积的性质,函数的奇偶性的判断,属于基础试题
分析:由已知可得,
 =
= ,然后结合函数的奇偶性即可检验
,然后结合函数的奇偶性即可检验解答:∵
 ,
,∴
 =
=
=

∴f(-x)=
 =f(x)
=f(x)∴f(x)是偶函数
故选D
点评:本题主要考查了向量的数量积的性质,函数的奇偶性的判断,属于基础试题

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 、
、 、
、 满足
满足 ,向量
,向量 ,且
,且 ,则向量
,则向量 B.
B. C.
C. D.
D.
 、
、 ,满足
,满足 等于
等于 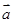 、
、 、
、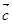 满足
满足 ,设向量
,设向量 ,则
,则