题目内容
已知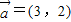 ,
,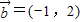 ,
,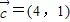 .
.(1)求向量
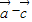 与向量
与向量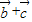 的夹角;
的夹角;(2)k为何值时,
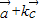 与
与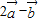 平行.
平行.
【答案】分析:(1)由坐标运算可得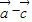 ,
,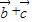 的坐标,可得数量积为0,可得夹角;(2)同理可得
的坐标,可得数量积为0,可得夹角;(2)同理可得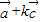 与
与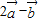 的坐标,由平行可得(4k+3)•2-(k+2)•7=0,解之即可.
的坐标,由平行可得(4k+3)•2-(k+2)•7=0,解之即可.
解答:解:(1)由题意可得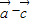 =(-1,1),
=(-1,1),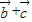 =(3,3)
=(3,3)
故可得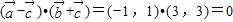 ,
,
故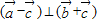 ,
,
即向量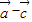 与向量
与向量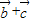 的夹角为90°.…(3分)
的夹角为90°.…(3分)
(2)由题意可得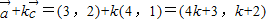 ,
,
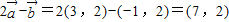 ,
,
要满足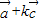 与
与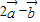 平行,需满足(4k+3)•2-(k+2)•7=0
平行,需满足(4k+3)•2-(k+2)•7=0
解之可得:k=8
点评:本题考查平面向量的基本运算,涉及向量的夹角公式和向量共线的条件,属中档题.
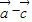 ,
,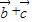 的坐标,可得数量积为0,可得夹角;(2)同理可得
的坐标,可得数量积为0,可得夹角;(2)同理可得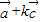 与
与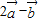 的坐标,由平行可得(4k+3)•2-(k+2)•7=0,解之即可.
的坐标,由平行可得(4k+3)•2-(k+2)•7=0,解之即可.解答:解:(1)由题意可得
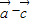 =(-1,1),
=(-1,1),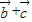 =(3,3)
=(3,3)故可得
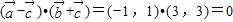 ,
,故
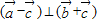 ,
,即向量
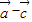 与向量
与向量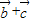 的夹角为90°.…(3分)
的夹角为90°.…(3分)(2)由题意可得
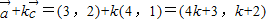 ,
,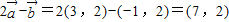 ,
,要满足
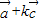 与
与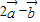 平行,需满足(4k+3)•2-(k+2)•7=0
平行,需满足(4k+3)•2-(k+2)•7=0解之可得:k=8
点评:本题考查平面向量的基本运算,涉及向量的夹角公式和向量共线的条件,属中档题.

练习册系列答案
相关题目
 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2). ,函数
,函数
 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在 上的值域.
上的值域.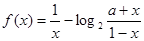 为奇函数.
为奇函数.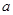 的值;
的值;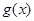 的图象由函数
的图象由函数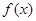 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出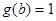 ,求
,求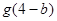 的值.
的值.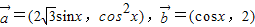 ,函数
,函数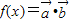
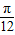 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在
倍,纵坐标不变,得到函数y=g(x)的图象.求g(x)在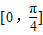 上的值域.
上的值域. ,函数
,函数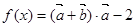
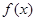 的最小正周期
的最小正周期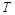 ;
;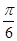 上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数
上个单位后,再将所得图像上所有点的横坐标伸长为原来的3倍,得到函数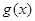 的图像,求函数
的图像,求函数