题目内容
已知抛物线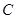 :
: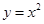 .过点
.过点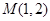 的直线
的直线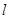 交
交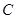 于
于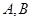 两点.抛物线
两点.抛物线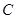 在点
在点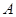 处的切线与在点
处的切线与在点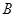 处的切线交于点
处的切线交于点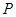 .
.
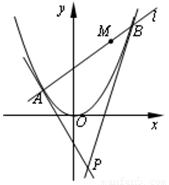
(Ⅰ)若直线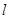 的斜率为1,求
的斜率为1,求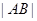 ;
;
(Ⅱ)求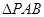 面积的最小值.
面积的最小值.
【答案】
(1)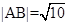 ;(2)最小值为2.
;(2)最小值为2.
【解析】
试题分析:本题主要考查直线与抛物线的位置关系、三角形面积公式等基础知识,同时考查解析几何的基本思想方法和运算求解能力.第一问,由已知得出直线l的方程,与抛物线联立,得出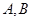 两点的坐标,然后利用两点间距离公式求
两点的坐标,然后利用两点间距离公式求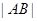 ;第二问,由于直线l的斜率不知道,所以设出直线方程,设出点
;第二问,由于直线l的斜率不知道,所以设出直线方程,设出点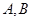 的坐标,联立直线与抛物线方程,得出两根之和,两根之积,设出在点
的坐标,联立直线与抛物线方程,得出两根之和,两根之积,设出在点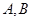 处的切线方程,求出交点
处的切线方程,求出交点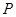 的坐标,利用点到直线的距离公式求出
的坐标,利用点到直线的距离公式求出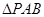 的高,再求
的高,再求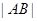 ,代入到三角形面积公式中,再把两根之和,两根之积代入得到关于
,代入到三角形面积公式中,再把两根之和,两根之积代入得到关于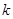 的表达式,利用配方法求最值.
的表达式,利用配方法求最值.
试题解析:(Ⅰ)由题意知,直线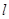 的方程为
的方程为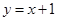 ,由
,由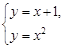 消去
消去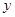 解得
解得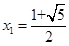 ,
, 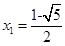 .
.
所以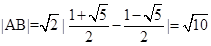 .
6分
.
6分
(Ⅱ)设直线l的方程为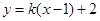 ,设点
,设点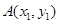 ,
,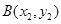 .
.
由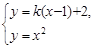 消去
消去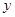 整理得
整理得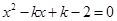 ,
,
知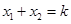 ,
, 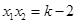 ,
,
又因为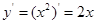 ,所以,抛物线
,所以,抛物线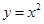 在点
在点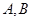 处的切线方程分别为
处的切线方程分别为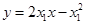 ,
,
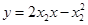 .
.
得两切线的交点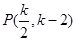 .所以点
.所以点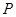 到直线
到直线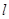 的距离为
的距离为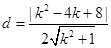 .
.
又因为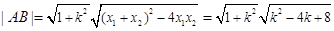 .
.
设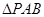 的面积为
的面积为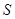 ,所以
,所以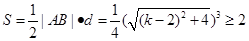 (当
(当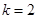 时取到等号).
时取到等号).
所以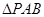 面积的最小值为2.
14分
面积的最小值为2.
14分
考点:1.直线与抛物线的位置关系;2.三角形面积公式;3.点到直线的距离公式;4.两点间距离公式.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 过点A
过点A 
 过定点
过定点 ,斜率为
,斜率为 ,当
,当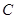 :
: ,过点
,过点 (其中
(其中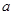 为正常数)任意作一条直线
为正常数)任意作一条直线 交抛物线
交抛物线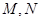 两点,
两点, 为坐标原点.
为坐标原点. 的值;
的值;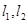 ,试探求
,试探求 与
与 的交点是否在定直线上,证明你的结论.
的交点是否在定直线上,证明你的结论. ,过点
,过点 作抛物线的两条切线
作抛物线的两条切线 ,切点分别为
,切点分别为 .
. 过定点
过定点 ;
; (
( 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.