题目内容
(本小题12分)已知抛物线C: 过点A
过点A 
(1)求抛物线C 的方程;
(2)直线 过定点
过定点 ,斜率为
,斜率为 ,当
,当 取何值时,直线
取何值时,直线 与抛物线C只有一个公共点。
与抛物线C只有一个公共点。
【答案】
(I) ;(2)当
;(2)当 时,直线
时,直线 与抛物线C只有一个公共点。
与抛物线C只有一个公共点。
【解析】
试题分析:(Ⅰ)由题意设抛物线的方程为y2=2px,把A点坐标(1,-2)代入方程得P的值,由此能求出抛物线的标准方程.
(Ⅱ)由题意,直线l的方程为y=kx+2k+1,由方程组y2=4x和y=kx+2k+1联立,得ky2-4y+4(2k+1)=0,对于参数k进行分类讨论,这时直线l抛物线有一个公共点.
解:(I)将(1,-2)代入 ,得
,得 ,
,
所以p=2;故所求的抛物线C的方程为
(2)由 得:
得: ,
,
①当 时,
时, 代入
代入 得
得 ,
,
这时直线 与抛物线C相交,只有一个公共点
与抛物线C相交,只有一个公共点
②当 时,
时, ,时
,时
直线 与抛物线C相切,只有一个公共点
与抛物线C相切,只有一个公共点
综上,当 时,直线
时,直线 与抛物线C只有一个公共点。
与抛物线C只有一个公共点。
考点:本试题主要考查了抛物线方程的求解,以及直线与抛物线的位置关系的综合运用。
点评:解决该试题的关键是利用点求解解析式,同时能结合二次方程研究方程根的问题。

练习册系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线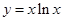
 处的切线方程。
处的切线方程。