题目内容
已知顶点是坐标原点,对称轴是 轴的抛物线经过点
轴的抛物线经过点 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)直线 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线 的方程.
的方程.
【答案】
(1) ;(2)
;(2) 或
或 .
.
【解析】本试题主要考查了抛物线的方程和直线与抛物线的位置关系的运用。第一问,利用设抛物线的方程为 ,代入点
,代入点 ,得到
,得到 ,解得。
,解得。
第二问中,设直线 的方程为
的方程为 联立方程组,结合韦达定理可知
联立方程组,结合韦达定理可知
= =
= ,得到k 的值。
,得到k 的值。
解:(Ⅰ)由题意设抛物线的方程为 ,
,
把A点坐标 代入方程得
代入方程得 ,
,
解得 ,所以抛物线的标准方程是
,所以抛物线的标准方程是 . ………………………………4分
. ………………………………4分
(Ⅱ)由题意,直线 的方程为
的方程为
由方程组 得
得 .
………………………6分
.
………………………6分
设A,B两点的坐标分别为
则
所以
= =
= ,
,
因为 ,所以
,所以 ,
,
解得, ,
…………………………10分
,
…………………………10分
所以直线 的方程为
的方程为 即
即 或
或 . ……………12分
. ……………12分

练习册系列答案
相关题目
 轴的抛物线经过点
轴的抛物线经过点 .
. 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线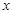 轴的抛物线经过点A
轴的抛物线经过点A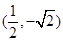 .
.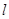 过定点
过定点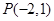 ,斜率为
,斜率为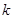 ,当
,当