题目内容
已知顶点是坐标原点,对称轴是x轴的抛物线经过点A(
,-
).
(Ⅰ)求抛物线的标准方程.
(Ⅱ)直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线有两个公共点?
| 1 |
| 2 |
| 2 |
(Ⅰ)求抛物线的标准方程.
(Ⅱ)直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线有两个公共点?
(本小题满分13分)
(Ⅰ)由题意设抛物线的方程为y2=2px,
把A点坐标(
,-
)代入方程得(-
)2=2p×
,
解得p=2,
所以抛物线的标准方程是y2=4x
(Ⅱ)由题意,直线l的方程为y=kx+2k+1
由方程组
,
得ky2-4y+4(2k+1)=0,
显然k=0不满足题意,∴k≠0
于是由△=-16(2k2+k-1)>0,
即2k2+k-1<0,
解得 -1<k<
于是,当-1<k<
,
且k≠0时,以上方程组有两个解,这时直线l抛物线有两个公共点.
故当k≠0时,直线l与抛物线有两个公共点.
(Ⅰ)由题意设抛物线的方程为y2=2px,
把A点坐标(
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解得p=2,
所以抛物线的标准方程是y2=4x
(Ⅱ)由题意,直线l的方程为y=kx+2k+1
由方程组
|
得ky2-4y+4(2k+1)=0,
显然k=0不满足题意,∴k≠0
于是由△=-16(2k2+k-1)>0,
即2k2+k-1<0,
解得 -1<k<
| 1 |
| 2 |
于是,当-1<k<
| 1 |
| 2 |
且k≠0时,以上方程组有两个解,这时直线l抛物线有两个公共点.
故当k≠0时,直线l与抛物线有两个公共点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 轴的抛物线经过点
轴的抛物线经过点 .
. 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线 轴的抛物线经过点
轴的抛物线经过点 .
. 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线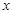 轴的抛物线经过点A
轴的抛物线经过点A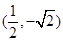 .
.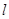 过定点
过定点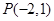 ,斜率为
,斜率为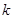 ,当
,当