题目内容
已知顶点是坐标原点,对称轴是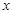 轴的抛物线经过点A
轴的抛物线经过点A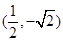 .
.
(Ⅰ)、求抛物线的标准方程.
(Ⅱ)、直线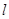 过定点
过定点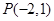 ,斜率为
,斜率为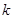 ,当
,当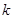 为何值时,直线
为何值时,直线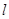 与抛物线有两个公共点?
与抛物线有两个公共点?
【答案】
20、(本小题满分12分)
解:(Ⅰ)、由题意设抛物线的方程为 ,
,
把A点坐标 代入方程得
代入方程得 ,
,
解得 ,所以抛物线的标准方程是
,所以抛物线的标准方程是
(Ⅱ)、由题意,直线 的方程为
的方程为
由方程组 得
得
显然 不满足题意, ∴
不满足题意, ∴
于是由△= ,即
,即 解得
解得 
于是,当 ,且
,且 时,以上方程组有两个解,这时直线
时,以上方程组有两个解,这时直线 抛物线有两个公共点
抛物线有两个公共点
【解析】略

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 轴的抛物线经过点
轴的抛物线经过点 .
. 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线 轴的抛物线经过点
轴的抛物线经过点 .
. 过点
过点 ,且与抛物线交于不同两点A,B,若
,且与抛物线交于不同两点A,B,若 ,求直线
,求直线