Question

如右图，在三棱锥P—ABC中，PC⊥底面ABC，AB⊥BC，D，E分别是AB，PB的中点．PC=1，BC=1.

（1）求证：DE∥平面PAC；（5分）

（2）求证：AB⊥PB；（5分）

（3）求点C到平面ABP的距离.（4分）

Answer 1

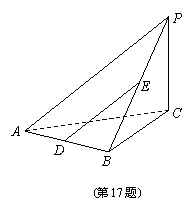
 (1)证明：D，E分别是AB，PB的中点，DE∥AP． ………………2分

AP平面PAC，且DE平面PAC，

DE∥平面PAC                              ……………………………………5分

(2) 证明：PC⊥平面ABC，AB平面ABC  PC⊥AB        ……………………7分

AB⊥BC，且PC∩BC＝C，PC、BC平面PBC

AB⊥平面PBC               ------------9分

PB平面PBC，AB⊥PB    ------------10分

(3) 解：PC⊥平面ABC，BC平面ABC  PC⊥BC

在中，由勾股定理得,

PB=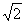                             ……………………………………11分

由（2）证知是直角三角形，

设点C到平面PAB的距离为h,由等体积法得：

即,=

即点C到平面PAB的距离为.                     ………………………………………14分