题目内容

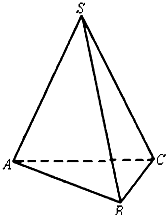精英家教网在三棱锥S-ABC中，SA=SB=SC=1，∠ASB=∠ASC=∠BSC=30°，如图，一只蚂蚁从点A出发沿三棱锥的表面爬行一周后又回到A点，则蚂蚁爬过的最短路程为
 
．
分析：画出解答几何体的部分侧面展开图，利用直角三角形的边的关系容易解得斜边的值，从而得出其中的最小值．
解答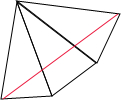：精英家教网解：将三棱锥S-ABC沿侧棱AS展开，
其侧面展开图如图所示，由图中红色路线可得结论．
故答案为：
2
点评：本题考查多面体和旋转体表面上的最短距离问题，空间想象能力，几何体的展开与折叠，是基础题．
练习册系列答案
相关题目
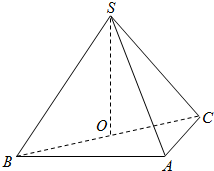精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为边长为1的等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）证明：SA⊥BC；
（Ⅲ）求三棱锥S-ABC的体积．
精英家教网如图，在三棱锥S-ABC中，侧面SAB与侧面SAC均为等边三角形，∠BAC=90°，O为BC中点．
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求二面角A-SC-B的余弦值．
精英家教网如图，在三棱锥S-ABC中，侧面SAB⊥底面ABC，且∠ASB=∠ABC=90°，AS=SB=2，AC=2
3
．

（Ⅰ）求证SA⊥SC；
（Ⅱ）在平面几何中，推导三角形内切圆的半径公式r=
2S
l
（其中l是三角形的周长，S是三角形的面积），常用如下方法（如右图）：
①以内切圆的圆心O为顶点，将三角形ABC分割成三个小三角形：△OAB，△OAC，△OB精英家教网C．
②设△ABC三边长分别为a，b，c．由S△ABC=S△OBC+S△OAC+S△OAB，
得S=
1
2
ar+
1
2
br+
1
2
cr=
1
2
lr，则r=
2S
l
．
类比上述方法，请给出四面体内切球半径的计算公式（不要求说明类比过程），并利用该公式求出三棱锥S-ABC内切球的半径．
如图，在三棱锥S-ABC中，SA=AB=BC=AC=
2
SB=
2
SC，O为BC中点．
（1）求证：SO⊥平面ABC
（2）在线段AB上是否存在一点E，使二面角B-SC-E的平面角的余弦值为
15
5
？若存在，确定E点位置；若不存在，说明理由．
在三棱锥S-ABC中，侧棱SC⊥平面SAB，SA⊥BC，侧面△SAB，△SBC，△SAC的面积分别为1，
3
2
，3，则此三棱锥的外接球的表面积为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网