题目内容
（2012•泰州二模）选修4-1：几何证明选讲如图，⊙O的直径AB的延长线与弦CD的延长线相交于点P，E为⊙O上一点，AE=AC，求证：∠PDE=∠POC．
分析：因AE=AC，AB为直径，可得∠OAC=∠OAE，由∠POC=∠OAC+∠OCA=∠EAC．及由EACD四点共圆可得∠EAC=∠PDE，从而可证
解答：证明：因AE=AC，AB为直径，
所以，弧EB与弧BC相等
由于同一个圆中，等弧所对的圆周角相等
故∠OAC=∠OAE． …（3分）
因为OA=OC
所以∠OAC=∠OCA
因为∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC．
因为EACD四点共圆
所以，∠EAC=∠PDE，
所以，∠PDE=∠POC．…（10分）
所以，弧EB与弧BC相等
由于同一个圆中，等弧所对的圆周角相等
故∠OAC=∠OAE． …（3分）
因为OA=OC
所以∠OAC=∠OCA
因为∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC．
因为EACD四点共圆
所以，∠EAC=∠PDE，
所以，∠PDE=∠POC．…（10分）
点评：本题主要考查了圆周角定理及圆内接四边形的性质定理的应用，证明此类问题要求考试熟练掌握基本定理．
练习册系列答案
相关题目
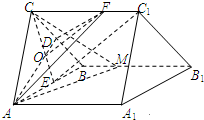（2012•泰州二模）如图，三棱柱ABC-A1B1C1中，D、E分别是棱BC、AB的中点，点F在棱CC1上，已知AB=AC，AA1=3，BC=CF=2．