题目内容
(2012•泰州二模)已知角φ的终边经过点P(1,-2),函数f(x)=sin(ωx+φ)(ω>0)图象的相邻两条对称轴之间的距离等于
,则f(
)=
| π |
| 3 |
| π |
| 12 |
-
| ||
| 10 |
-
.
| ||
| 10 |
分析:由已知中角φ的终边经过点P(1,-2),可求出φ角的正弦值和余弦值,由函数f(x)图象的相邻两条对称轴之间的距离等
,可求出函数的周期,进而求出ω,将
,代入函数的解析式,利用两角和的正弦公式,展开计算可得答案.
| π |
| 3 |
| π |
| 12 |
解答:解:函数f(x)=sin(ωx+φ)图象的相邻两条对称轴之间的距离等于
,
∴函数f(x)的周期T=
,
∵ω>0
∴ω=3
∵角φ的终边经过点P(1,-2),
∴sinφ=
,cosφ=
∴f(
)=sin(3•
+φ)=sin(
+φ)=
(sinφ+cosφ)=
•(
)=-
故答案为:-
| π |
| 3 |
∴函数f(x)的周期T=
| 2π |
| 3 |
∵ω>0
∴ω=3
∵角φ的终边经过点P(1,-2),
∴sinφ=
-2
| ||
| 5 |
| ||
| 5 |
∴f(
| π |
| 12 |
| π |
| 12 |
| π |
| 4 |
| ||
| 2 |
| ||
| 2 |
-
| ||
| 5 |
| ||
| 10 |
故答案为:-
| ||
| 10 |
点评:本题考查的知识点正弦型函数解析式的求法,函数的值,其中熟练掌握三角函数的定义及正弦型函数的图象和性质是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
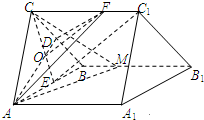 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.