题目内容
若数列x,a1,a2,y成等差数列,x,b1,b2,y成等比数列,则 的取值范围是________.
的取值范围是________.
[4,+∞)或(-∞,0]
分析:由题意可知 =
= =
= =
= +
+ +2.由此可知
+2.由此可知 的取值范围.
的取值范围.
解答:在等差数列中,a1+a2=x+y;在等比数列中,xy=b1•b2.
∴ =
= =
= =
= +
+ +2.
+2.
当x•y>0时, +
+ ≥2,故
≥2,故 ≥4;
≥4;
当x•y<0时, +
+ ≤-2,故
≤-2,故 ≤0.
≤0.
答案:[4,+∞)或(-∞,0]
点评:本题考查数列的性质和应用,解题时要认真审题,仔细思考.
分析:由题意可知
 =
= =
= =
= +
+ +2.由此可知
+2.由此可知 的取值范围.
的取值范围.解答:在等差数列中,a1+a2=x+y;在等比数列中,xy=b1•b2.
∴
 =
= =
= =
= +
+ +2.
+2.当x•y>0时,
 +
+ ≥2,故
≥2,故 ≥4;
≥4;当x•y<0时,
 +
+ ≤-2,故
≤-2,故 ≤0.
≤0.答案:[4,+∞)或(-∞,0]
点评:本题考查数列的性质和应用,解题时要认真审题,仔细思考.

练习册系列答案
相关题目
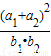 的取值范围是 .
的取值范围是 .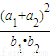 的取值范围是 .
的取值范围是 .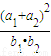 的取值范围是 .
的取值范围是 .